Pragmatik
Jetzt wollen wir einen Teil unserer Belohnung genießen. Nachdem wir die Prinzipien der richtigen Diagnosestellung begriffen haben, können wir uns jetzt Problemen zuwenden, an denen bisher sehr viel Akademiker gescheitert sind. Egal, ob es sich um Ärzte, Juristen, Soziologen oder Psychologen handelte, viele Akademiker konnten einfache und sehr relevante Fragen nicht richtig beantworten. Einige dieser Probleme und deren Lösungen werden wir jetzt schildern.
Um 1970 untersuchten die Psychologen in ausgefeilten Studien, ob wir uns in unseren alltäglichen Beurteilungen auch an die Prinzipien der Wahrscheinlichkeitsrechnungen halten oder nicht. Dabei stießen die Forscher auf sehr interessante und zum Teil verblüffende Ergebnisse, die wir an dem berühmten „Taxiproblem“ erläutert werden.
Stellen wir uns folgende Situation vor: In einer Stadt gibt es zwei Taxiunternehmer, deren Taxis jeweils blau oder dunkelgrün sind. Alle Taxis sind durch beleuchtete Anzeigen auf dem Dach als Taxis sehr gut erkennbar. Ein Zeuge beobachtet, dass ein Taxi ein parkendes Auto rammt und danach Unfallflucht begeht. Bei der polizeilichen Befragung behauptet der Zeuge, das Taxi wäre blau gewesen. Ist durch den Augenzeugen zweifelsfrei bewiesen, dass es ein blaues Taxi war? Sicherlich nicht, denn wir wissen aus vielen Prozessen und Zeugenvernehmungen, wie anfällig und manipulierbar Zeugenaussagen sind. Wenn zehn Personen zufällig einen Unfall oder Überfall beobachten, an dem mehrere andere Personen beteiligt sind, und diese zehn Personen müssen dann die Beteiligten beschreiben, dann divergieren die Beschreibungen sehr stark. Ein eindeutige, übereinstimmende und zielführende Täter- oder Verlaufsbeschreibung ist äußerst selten.

Tab. 24-1 Beobachtungsvermögen des Zeugens in der Dämmerung
Da der Unfall in der abendlichen Dämmerung stattfand und die Verlässlichkeit des Zeugen bezweifelt wird, veranlasst der Richter in unserem Beispiel einen Ortstermin und lässt 20 Taxis vorfahren: zehn grüne und zehn blaue. Dabei zeigt sich, dass der Zeuge in 80 Prozent der Fälle die Farbe richtig erkennt (Tab. 24-1). Wie wahrscheinlich ist es nun, dass der Zeuge tatsächlich ein blaues Taxi gesehen hat? Bitte antworten Sie jetzt nicht 80 Prozent, denn dann greift eine ähnliche Regel wie aus dem Spiel „Monopoly“: „Gehe zurück zu Kap. 22. Gehe nicht zum Ende des Buches und erhalte auch keine Belohnung“.
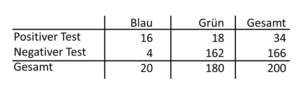
Tab. 24-2 Sensitivität und Spezifität des Zeugen von jeweils 80 Prozent
Warum ist die Wahrscheinlichkeit nicht einfach 80 Prozent, obgleich die Tabelle es nahelegt? Die suggerierten 80 Prozent basieren auf dem Ortstermin mit 20 Taxis, der anberaumt wurde, um quasi die Sensitivität und Spezifität des Zeugen zu bestimmen. Aber spätestens jetzt sollte uns ein Licht aufgehen, denn die Sensitivität benötigen wir hier nicht, sondern die positiven Vorhersagewerte. Und diese wiederum hängen von der Prävalenz ab. Wir haben nämlich bisher stillschweigend unterstellt, dass beide Taxiunternehmen mit gleich vielen Taxis in der Stadt unterwegs sind. In dem Ortstermin haben wir deshalb auch jeweils 10 Taxis aus jedem Unternehmen vorfahren lassen. Diese gleiche Verteilung entspricht aber nicht den Tatsachen. Das grüne Taxiunternehmen ist sehr viel umfangreicher und beherrscht die Stadt. 90 Prozent aller Taxis sind grün.
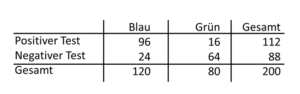
Tab. 24-3 Sensitivität und Spezifität des Zeugen von jeweils 80 Prozent
Ändert diese Information unsere Einschätzung, welche Farbe das Taxi wahrscheinlich gehabt haben könnte? Natürlich, denn wir erhalten jetzt eine andere Situation, wenn es 200 Taxis in der Stadt gibt, von denen 180 grün sind (Tab. 24-2). Wir sehen jetzt auf einen Blick, dass der Zeuge wahrscheinlich eher ein grünes Taxi gesehen hat, dass er falsch-positiv als blaues Taxi identifizierte. Denn von den 34 als blau identifizierte Taxis waren nur 16 tatsächlich blau und 18 grün.
Es hätte natürlich aus sein können, dass es mehr blaue Taxis in der Stadt gibt. Wenn es 120 blaue Taxis und 80 grüne Taxis geben würde, dann würde sich die Situation drastisch umkehren (Abb. 24-3). Die Wahrscheinlichkeit, dass es tatsächlich ein blaues Taxi ist, das der Zeuge gesehen hat, betrüge dann 96/112.
Was können wir aus dem Taxi-Problem lernen? Ohne Wissen über die Prävalenz und die Verlässlichkeit des Zeugens sind wir eigentlich blind und können die Zeugenaussage nicht sinnvoll verwerten. Dennoch vergessen wir häufig, die Prävalenz in unsere Gedanken aufzunehmen. Wir vertrauen direkt der Zeugenaussage, weil wir uns selbst auch vertrauen würden. Wir realisieren nicht, dass unsere unsicheren Kenntnisse auch davon abhängen, in welcher Umgebung wir uns befinden bzw. in welcher konkreten Konstellation bestimmte Ereignisse gerade auftreten.
Üben wir das an einem anderen Beispiel. Stellen wir uns vor, dass nach einer Vergewaltigung eine DNS-Probe des Täters vorliegt. Der Täter wird zunächst nicht gefunden. Aufgrund von zufälligen Untersuchungen in Krankenhäusern wird nach zwei Jahren festgestellt, dass es eine Übereinstimmung der DNS gibt. Ist damit der Täter identifiziert?
Wir unterstellen, dass die Wahrscheinlichkeit sehr gering ist (0,01 Prozent), dass zwei Menschen dieselben untersuchten DNS-Stränge haben. Zu 99,99 Prozent sind die Stränge verschieden, was 1:10.000 entspräche. Können wir jetzt behaupten, dass der Täter zu 99,99 Prozent identifiziert ist? Auch hier hängt die Antwort von der Prävalenz ab. Wenn wir davon ausgehen, dass ungefähr 1 Million Einwohner in Betracht gekommen wären, die Tat verübt zu haben, dann sind immerhin 100 Personen darunter, die als Täter in Frage kämen – von denen wir jetzt einen gefunden haben. Wäre der Kreis der Verdächtigen dagegen bereits durch andere Indizien auf 100 Personen beschränkt, dann hätte die DNS-Analyse eine hohe Beweiskraft. Aus diesen Beispielen lernen wir, dass wir zuerst die erforderliche Umsicht walten lassen sollten, bevor wir ein vorschnelles Urteil fällen.
Warum wird die Prävalenz in der Bewertung häufig vergessen? Warum denken wir nicht so, wie es die Wahrscheinlichkeitsrechnung nahelegt? Warum sind wir keine intuitiven Statistiker? Warum fällt es uns so schwer, in Wahrscheinlichkeitsräumen zu denken? Gerd Gigerenzer und seine Arbeitsgruppe weisen immer wieder daraufhin, dass Akademiker zu einer korrekten Einschätzung gelangen, wenn man ihnen einfache Häufigkeiten statt Wahrscheinlichkeiten nennt. Deshalb ist es immer hilfreich, die tatsächlichen absoluten Zahlen graphisch oder in einer Tabelle abzubilden.