Numerische Werte und ROC-Kurven
Nachdem wir weiter über unseren Korridor schlendern, finden wir eine weitere Tür, auf der „ROC-Kurven“ geschrieben steht. Neugierig, wie wir sind, öffnen wir auch diese Tür. Wir betreten einen futuristischen Raum, in dem es von komplexen, laut ratternden Maschinen nur so wimmelt. Gleich rechts sehen wir eine Maschine mit der Aufschrift „Diabetes mellitus“ mit einem großen roten Schieberegler. Wir bewegen ihn auf und ab und bemerken dabei, dass sich unentwegt Zahlen auf einem großen Bildschirm ändern. Eine andere Maschine heißt „Schilddrüsenunterfunktion“ mit einem überdimensionierten grünen Schieberegler, auf dem „TSH“ steht. Auch hier ändern sich Zahlenkolonnen, wenn wir den Schieberegler auf und ab bewegen. Etwas verwirrt, versuchen wir die inhärente Systematik zu ergründen. Da es uns nicht gelingt, verlassen wir enttäuscht den Raum.
Auf dem Korridor bemerken wir direkt daneben eine Tür mit der Aufschrift „Interpretation von Laborwerten“. Bisher haben wir ausschließlich einfache Testverfahren besprochen, die die Ergebnisse „ja“ oder „nein“ bzw. „negativ“ oder „positiv“ zuließen, denn die bisher besprochenen Gütekriterien einer diagnostischen Untersuchung werden letztlich so definiert. Allerdings lernten wir zuletzt mit den Likelihood Ratios auch ein Bewertungsverfahren kennen, das sich bei weiter differenzierten Testverfahren mit mehreren Klassifikationen anwenden ließ. Im klinischen Alltag sind solche einfachen Ergebnisse aber in der Minderheit. Wir haben es häufiger mit numerischen Werten zu tun, denen wir uns jetzt zuwenden. Zum Beispiel bestimmen wir im Rahmen der Nachsorge von Patienten mit Dickdarmkrebs den CEA-Wert (Carcino-Embryonales Antigen). Nehmen wir an, der Wert beträgt 12,2 ng/ml. Wie bewerteten wir das Ergebnis? Ist der Wert als negativ zu interpretieren? Sind wir beunruhigt? Betrachten wir einen anderen Patienten, der seit gestern über rechtsseitige Oberbauchschmerzen klagt. Wir messen unter anderem die alkalische Phosphatase, um eine Stauung der Gallenwege (Cholestase) auszuschließen. Der Wert beträgt 251 IU/l. Wir interpretieren den Wert als positiv und veranlassen eine Ultraschalluntersuchung der Gallenwege, um das Ausmaß der Stauung und die mögliche Ursache zu bestimmen. Ein anderer Patient fühlte sich nach einer Schilddrüsenentfernung sehr abgeschlagen und wir überprüfen die Hormonlage, indem wir den TSH-Wert messen. Der Wert beträgt 4,4 mU/l. Fühlen wir uns bestätigt?
Es scheint so zu sein, dass wir numerische Werte ähnlich verwenden wie Likelihood Ratios. Wir vermuten eine Erkrankung und verschieben unsere Vortestwahrscheinlichkeit je nach der Höhe des Laborwertes. Ist das gerechtfertigt? Laborwerte sind schließlich keine LR.
Werfen wir einen erneuten Blick auf unseren Umgang mit Laborwerten. Wir verknüpfen mit numerischen Werten häufig so etwas wie Bestätigung oder Widerlegung unserer klinischen Vermutung. Stark erhöhte oder erniedrigte Werte erscheinen uns eindeutig und helfen, klare Diagnosen zu stellen. Manchmal befinden sich die Werte aber auch in einem indifferenten Bereich, wo wir dem Wert keine sichere diagnostische „Kraft“ zusprechen, weil er eben einen gewissen Schwellenwerte nicht über- oder unterschritten hat. Erst wenn der Wert sich jenseits einer bestimmten Schwelle befindet, dann sprechen wir ihm eine Aussagekraft zu. Wir fühlen uns erst jenseits dieser Schwelle bestätigt oder widerlegt und entscheiden erst dann, dass der Patient erkrankt ist oder nicht. Wir enden also bei numerischen Werten immer bei einer Trichotomie „ja, vielleicht oder nein“ bzw. „positiv, indifferent oder negativ“.
Woher generieren wir diese Schwellenwerte und was ändert sich, wenn wir die Schwellenwerte ändern? Schwellenwerte sind unerlässlich, um numerische Werte so zu interpretieren, dass man aus ihnen praktische Schlussfolgerungen ziehen kann. Wenn wir auf dem Aktienmarkt investieren, dann sind wir gewohnt, ab einem Schwellenwert zu kaufen oder zu verkaufen. Schwanken unsere Aktien zwischen diesen Werten, dann beobachten wir das wohlwollend und hoffen auf einen Anstieg. Aber wir würden hier doch nicht bei einem geringen Abfall sofort panikartig die Aktie verkaufen.

Abb. 22-1 Blutzuckerwerte in mg/dl von Gesunden (n=982) und Diabetikern (n=1075)
Ähnlich ist es in der Medizin. Nehmen wir an, wir vermuten eine akute Entzündung der Gallenblase bei einem Patienten mit rechtsseitigen Oberbauchschmerzen und erkennen eine verdickte Gallenblasenwand in der Sonographie ohne typische Dreischichtung der Wand. Wir wollen unsere Verdachtsdiagnose bestätigen und bestimmen die Zahl der weißen Blutkörperchen (Leukozyten). Ab welchen Wert fühlen wir uns bestätigt? Ab welchen Wert würden wir unsere Diagnose in Frage stellen? Und bei welchen Werten würden wir uns so unsicher fühlen, dass wir uns nicht festlegen würden? Würden wir unsere Diagnose bei Werten unter 10,0 TI/nl revidieren und bei über 16,0 TI/nl bestätigt sehen? Oder sollten wir andere Werte wählen? Und wenn ja, warum? Würden wir vielleicht auch bei einer Leukozytenzahl von 10,0 TI/nl und stärksten lokalen Druckschmerzen auf unserer Diagnose beharren? Wie noch an weiteren Beispielen deutlich werden wird, setzen wir unsere Schwellenwerte gezielt ein und verändern sie unter anderen Rahmenbedingungen.
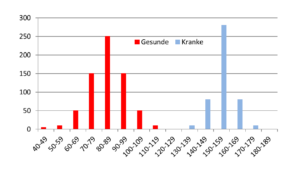
Abb. 22-2 Blutzuckerwerte in mg/dl bei Gesunden und Kranken
Die Ergebnisse eines fiktiven Szenarios: An einem Morgen wurde der Blutzucker von 982 Gesunden und von 1075 Diabetikern gemessen. Die Ergebnisse sind in Abbildung 22-1 dargestellt. Die Laborwerte schwanken bei den Gesunden und den Kranken und überlagern sich gegenseitig. Es gibt demnach keinen Schwellenwert, der eindeutig definiert, wann jemand sicher krank ist. Solch einen Schwellenwert würde es nur geben, wenn die beiden Gruppen sich eindeutig unterscheiden würden. In der Abbildung 22-2 wurde solch eine strikte Trennung simuliert. Ein Wert über 125 mg/dl bestätigt sicher die Diagnose der Erkrankung.
In unserem Beispiel trifft das leider nicht zu, so dass wir uns hier anders behelfen müssen. Wir definieren zunächst einen Schwellenwert von 80 mg/dl. Dazu denken wir uns bei 80 mg/dl einen dicken schwarzen Strich in der Abbildung 24-1. Alle, die sich links vom Strich bzw. unterhalb des Schwellenwertes befinden, sind gesund, und alle, die sich rechts vom Strich bzw. oberhalb des Schwellenwertes befinden, sind krank. Für diesen Schwellenwert können wir jetzt eine Vier-Felder-Tabelle anfertigen (Tabelle 22-1), um die Sensitivität und Spezifität zu berechnen. Man erkennt leicht, dass alle Kranken richtig erkannt wurden und die Sensitivität 100 Prozent beträgt. Leider wurden auch sehr viele Gesunde als krank angesehen, so dass die Spezifität nur 16,6 Prozent beträgt.
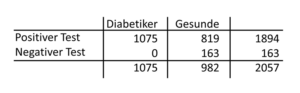
Tab. 22-1 Diabetiker bei einem Schwellenwert von 80 mg/dl
In einem nächsten Schritt erhöhen wir den Schwellenwert um 10 mg/dl. Dabei übersehen wir zwar einige Kranke, aber wir erkennen mehr Gesunde als richtig. Die Sensitivität sinkt etwas und die Spezifität steigt. Nun erhöhen wir den Schwellenwert jeweils um 10 mg/dl und rechnen für jeden Schritt die Sensitivität und Spezifität aus. Die Ergebnisse tragen wir in die Tabelle 22-2 ein. Wir beenden die Berechnung erst bei 170 mg/dl. In dieser Situation werden alle Patienten links von der gedachten Linie als gesund angesehen und alle rechts davon als krank. Hier wurden natürlich alle Gesunden richtig erkannt, so dass die Spezifität 100 Prozent beträgt. Leider wurden viele Kranke für gesund erklärt, so dass die Sensitivität auf 9,6 Prozent gesunken ist.
Betrachten wir nun unsere Werte in der Tabelle 22-2. Offensichtlich sinkt die Sensitivität kontinuierlich von 100 Prozent auf 9,6 Prozent und die Spezifität steigt kontinuierlich von 16,6 Prozent auf 100 Prozent an, wenn wir den Schwellenwert erhöhen. Dadurch ändern sich natürlich auch die LR+ und LR-. Diesen Zusammenhang zwischen der Sensitivität und der Spezifität bei numerischen Werten müssen wir immer berücksichtigen. Es ist äußerst wichtig, zu wissen, bei welchem Schwellenwert der Schieberegler gerade steht. Ohne die Angabe des Schwellenwertes sind die Gütekriterien nicht sinnvoll interpretierbar. Aber selbst das ist nicht hinreichend, wenn wir die diagnostische Qualitäten verschiedener Laborwerte bewerten wollen, denn wir müssten eigentlich die gesamte Tabelle 22-2 betrachten.
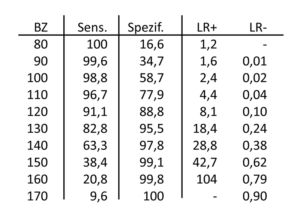
Tab. 22-2 Sensitivität, Spezifität, LR+ und LR- für verschiedene Schwellenwerte des Blutzuckers in mg/dl
Wenden wir uns noch einmal den LR+ und LR- in der Tabelle 22-2 zu. Wir hatten zu Beginn dieses Abschnittes vermutet, dass wir Laborwerte ähnlich wie LR einsetzen: Je weiter die Laborwerte abweichen, umso stärker fühlen wir uns bestätigt oder widerlegt. Und genau das bildet sich in der Tabelle ab. Bei einem niedrigen Schwellenwert von 80 mg/dl ist die LR+ unbrauchbar niedrig, aber der LR- ist sehr gut. Wir fühlen uns eher gegen die Diagnose eingestellt. Mit zunehmendem Blutzuckerspiegel steigt der LR+ und damit nimmt die Diskrimination zugunsten des Diabetes mellitus zu. Der LR- steigt dagegen an und verliert somit deutlich an Aussagekraft.
Mit diesem Wissen ausgestattet, verlassen wir den Raum „Interpretation von Laborwerten“ und betreten nun mutig den Raum „ROC-Kurven“. Wir gehen zur Maschine „Diabetes mellitus“ und bewegen jetzt den roten Schieberegler, der die Schwellenwerte verändert. Auf dem Display lesen wir jetzt die beiden Zahlenkolonnen und deren Überschriften. Es handelt sich in der Tat um die Sensitivität auf der linken Seite des Displays, aber um (1-Spezifität) auf der rechten Seite des Displays. Warum dort nicht die Spezifität steht, offenbart sich uns noch nicht – die Gründe werden wir gleich erfahren. Außerdem sehen wir eine komische Kurve auf einem zweiten Display, die überschrieben ist mit „ROC-Kurve für den Blutzuckerwert zur Diagnose des Diabetes mellitus“. Irgendwie scheint die ROC-Kurve etwas mit dem Schieberegler zu tun zu haben, denn ein Punkt wandert mit der Bewegung des Schiebereglers entlang der Kurve.
Um den Zusammenhang zwischen Schwellenwert, Sensitivität und Spezifität graphisch optimal darzustellen, werden ROC-Kurven verwendet. „ROC“ ist eine Kurzformel für „Receiver Operating Characteristic“. Angeblich wurden diese Kurven im Zweiten Weltkrieg eingeführt, als man untersuchte, warum das amerikanische Radar die japanischen Bomber beim Angriff auf Pearl Habour so spät erkannte. Daraus entwickelte sich in den nächsten Jahrzehnten eine Signalentdeckungstheorie, deren Prinzipien auch auf medizinische Diagnosen gut anwendbar sind. Die ROC-Kurven liefern uns einen Maßstab, um die Qualität bei der Entdeckung von Signalen oder Diagnosen zu bewerten. Das ist zum Beispiel für den U-Bootkrieg genauso wichtig wie in der Medizin. Stellen wir uns vor, wir jagen auf einem Zerstörer feindliche U-Boote. Wir sehen häufig auf den Monitoren etwas blinken oder hören mit dem Sonar Geräusche, wissen aber bei einem schwachen Signal nicht, ob es sich um ein U-Boot handelt oder nicht. Würden wir bei jedem schwachen Signal Alarm gegeben, dann wäre das relativ unsinnig, weil sehr viele harmlose, natürliche Phänomene so schwache Signale bewirken. Es wäre auch nicht hilfreich, nur sehr starke und absolut sichere Signale zu berücksichtigen, weil dann bereits die Gefahr sehr groß wäre, dass wir vom U-Boot torpediert werden. Die Bandbreite reicht hier von einem schwachen bis zu einem starken Signal. Irgendwo dazwischen müssen wir einen Schwellenwert definieren, ab dem ein U-Boot-Alarm ausgelöst wird. Natürlich immer mit dem Risiko, dass es kein U-Boot oder bereits zu spät ist.
Im ärztlichen Alltag bewerten wir Laborwerte, die sich außerhalb des normalen Bereiches befinden, nicht gleichermaßen als krankhaft. Wir unterstellen, dass eine starke oder sogar extreme Abweichung eher mit einer Erkrankung verknüpft ist als eine geringe Abweichung. Das diagnostische Signal erscheint uns bei deutlichen Abweichungen klarer. Ab welchem Schwellenwert wir einen Wert als krankhaft ansehen, hängt zusätzlich von den Umständen ab. Troponin ist zum Beispiel ein Marker, der als Hinweis für eine Durchblutungsstörung der Herzkranzgefäße gilt. Ein gering-erhöhtes Troponin bei einem völlig beschwerdefreien Patienten bewerten wir anders als bei jemandem mit einer bekannten koronaren Herzkrankheit oder Schmerzen in der linken Brust. Wir adjustieren die Schwellenwerte bei unseren Patienten und verhalten uns so wie im U-Boot-Kampf. Wenn wir uns im heimatlichen Hafen aufhalten, verwenden wir andere Schwellenwerte, als wenn wir uns in feindlichen Gewässern aufhalten. Im ersten Fall würden wir auf eine erhöhte Spezifität Wert legen, weil ein feindlicher Angriff unwahrscheinlich ist. Im Kampfgebiet würde es sich dagegen empfehlen, einen Schwellenwert mit hoher Sensitivität zu wählen, damit wir das feindliche Schiff sicher und frühzeitig erkennen.
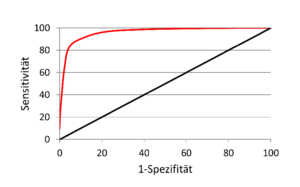
Abb. 22-3 ROC-Kurve des Blutzuckers zur Diagnose des Diabetes mellitus
Wenden wir uns jetzt den ROC-Kurven zu. Wie sehen ROC-Kurven aus? Wie wir uns erinnern, hatten wir mit den Likelihood Ratios einen guten Parameter, um die Aussagekraft eines Testes zu beurteilen. Die LR+ ist definiert als das Verhältnis „Sensitivität:(1-Spezifität)“. Es wird der Anteil der richtig-positiven Kranken zu den falsch-positiven Gesunden ins Verhältnis gesetzt. Dieses Verhältnis wird auch bei den ROC-Kurven genutzt. In einer ROC-Kurve wird in einer zweidimensionalen Graphik die Sensitivität gegen (1-Spezifität) für jeden gemessenen Schwellenwert aufgetragen. Unsere Tabelle 22-2 wird damit in die Abbildung 22-3 transformiert: Eine typische ROC-Kurve. Je mehr sich die Kurve im Bereich der Diagonale befindet, desto weniger ist sie geeignet, uns bei unserer Entscheidung zu helfen, ob der Patient erkrankt ist oder nicht. Die ROC-Kurve des perfekten Tests verläuft entlang der Y-Achse und schlägt in der linken oberen Ecke in die X-Achse um. Wir können auch die LR+ aus der Kurve ablesen, denn sie entsprechen der Steigung der Kurve an den Untersuchungspunkten. Die Steigung ist zunächst sehr groß und kippt dann relativ rasch in eine niedrige LR+.

Abb. 22-4 ROC-Kurven dreier verschiedener Laborwerte
Können wir aus der ROC-Kurve ablesen, wie gut wir mit dem Laborwert zwischen Kranken und Gesunden unterscheiden können? Ja, indem wir auf die Fläche unter der Kurve schauen. Diese Fläche ist ein Maß für die Diskriminationsfähigkeit des Testes. Ein Maß dafür, wie gut wir mit dem Laborwert zwischen krank und gesund tatsächlich unterscheiden können. Beträgt die Fläche nur die Hälfte (0,5) unter der eingezeichneten Diagonalen, dann ist der Test völlig wertlos. Werte von 1,0-0,9 gelten als exzellent, Werte von 0,9-0,8 als gut und Werte von 0,7-0,6 bereits als schlecht. Bereits graphisch können wir auf einen Blick den besseren Wert in der Abbildung 22-4 erkennen.
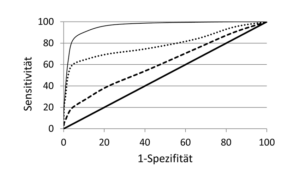
Abb. 22-5 ROC-Kurven des Troponin-I, Troponin-T und der Creatinkinase-MB
zur Diagnose des akuten Myokardinfarktes
Keller et al. Überprüften zum Beispiel, wie gut wir mit dem Troponin-I den frischen Herzinfarkt diagnostizieren können [Keller T et al. N Engl J Med 2009;361:868]. In der Abbildung 22-5 sind die ROC-Kurven für das Troponin-I, das Troponin-T und die Creatinkinase-MB nachgestellt. Die Abbildung zeigt auf einen Blick, dass das Troponin-I deutlich besser ist. Die Fläche unter der Kurve betrug für das Troponin-I 0,96, für das Troponin-T 0,85 und für die Creatinkinase-MB 0,67. Hier wird sehr deutlich, wie schlecht die CK-MB im Vergleich zum Troponin ist. Wenn wir in Zukunft die diagnostische Aussagekraft von numerischen Werten miteinander vergleichen, dann sollten die Ergebnisse als ROC-Kurven präsentiert werden. Nur die Sensitivität oder Spezifität bei einem definierten Schwellenwert anzugeben, ist nicht aussagekräftig.