Wer bis hierhin durchgehalten und alles verstanden hat, zählt bereits zu den großen Gewinnern. Wer jetzt noch zusätzlich wissen will, wann es überhaupt sinnvoll ist, einen Test durchzuführen, der sollte unbedingt weiterlesen.

Wir dehnen unsere Phantasie über den „Korridor der Diagnostik“ weiter aus und denken uns zwei weitere Türen hinzu, die linksseitig auf dem Korridor münden. Auf der ersten Tür steht „Eingang – Vor- und Nachtestwahrscheinlichkeit“ und auf der zweiten Tür „Ausgang – Vor- und Nachtestwahrscheinlichkeit“. An der zweiten Tür findet sich keine Türklinke. Sie scheint nur von innen geöffnet zu werden. Neugierig geworden, öffnen wir die erste Tür und betreten einen Raum, dessen Wände mit großen Postern ausgekleidet sind. Auf diesen Postern lesen wir zunächst eine Erläuterung. Dort steht: „Erkennen Sie, wie man im klinischen Alltag diagnostische Verfahren optimal einsetzt und welche Untersuchungsverfahren in der Situation am besten geeignet sind.“ Daneben findet sich eine Skizze über die Anordnung der Räume. Wir befinden uns offensichtlich im ersten von drei Räumen, die jeweils durch eine Tür miteinander verbunden sind. Die Türen gehen nur in eine Richtung auf, so dass wir gezwungen sein werden, durch die beiden anderen Räume zu gehen, um wieder in unseren Korridor zu gelangen.

Der erste Raum ist auf der Skizze mit „Vortestwahrscheinlichkeit“ beschriftet. Was ist darunter zu verstehen? Eine allgemeine Beschreibung der klinischen Situation steht an der Wand geschrieben: „Wenn Ärzte einem Patienten gegenüber stehen, dann führen sie in der Regel ein orientierendes Gespräch und untersuchen den Patienten. Danach haben sie mindestens eine Vermutung, woran der Patient leidet. Sie ordnen gezielte weitere Untersuchungen an, um die Vermutung zu bestätigen oder zu widerlegen. Wenn die Ärzte angeben müssten, mit welcher Wahrscheinlichkeit sie ihre Vermutung für wahr halten, dann entspräche diese Wahrscheinlichkeit der sogenannten Vortestwahrscheinlichkeit – eben der Wahrscheinlichkeit der Erkrankung vor dem Test.“

Die Vortestwahrscheinlichkeit ist ungefähr dasjenige, was wir mit der Prävalenz der Erkrankung im vorigen Abschnitt meinten. Wir werden im Folgenden an zwei Szenarien demonstrieren, wie wir die Begriffe „Vor- oder Nachtestwahrscheinlichkeit“ gewinnbringend einsetzen können. Im ersten Szenario ist der Hauptakteur ein 20jähriger Mann, der sich in der Rettungsstelle eines Krankenhauses vorstellt. Er klagte seit dem Vorabend über Übelkeit und ein Druckgefühl um den Nabel. Einige Stunden später bemerkte er Schmerzen im rechten Unterbauch, die über Stunden zunahmen. Bei der ärztlichen Untersuchung lässt sich im rechten Unterbauch ein starker Druckschmerz auslösen. Der Arzt vermutet aus der Vorgeschichte und Untersuchung eine Blinddarmentzündung (Appendizitis). Er ist sicher sehr sicher und gibt die Vortestwahrscheinlichkeit mit 95 Prozent an.

Im zweiten Szenario treffen wir auf eine 20jährige Frau, die seit Wochen immer wieder über rechtsseitige ziehende Bauchschmerzen klagte. Nach einer Party nahmen die Schmerzen zu, so dass sie sich jetzt in der Rettungsstelle vorstellt. Bei der ärztlichen Untersuchung lässt sich nur ein geringer Druckschmerz auslösen, wenn relativ stark gedrückt wurde. Der sonstige Bauchbefund ist unauffällig. Hier ist sich der Arzt nicht sicher. Er vermutet auch hier eine Blinddarmentzündung, die wahrscheinlich immer wieder „aufflammt“. Auf die Frage, wie sicher der Arzt mit seiner Diagnose ist, gibt er eine Vortestwahrscheinlichkeit von 40 Prozent an.

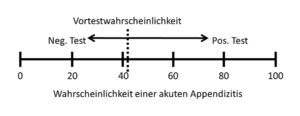Abb. 21-1   Ändern der Vortestwahrscheinlichkeit durch das Testergebnis

Im ersten Szenario beträgt die Vortestwahrscheinlichkeit 95 Prozent und im zweiten nur 40 Prozent. Es stellt sich nun die Frage, ob wir (als Ärzte) weitere Untersuchungen veranlassen sollten und wenn ja, welche? Beginnen wir mit dem „ob wir weitere Untersuchungen veranlassen sollen“. Wann halten wir weitere Untersuchungen überhaupt für erforderlich, nachdem wir bereits eine Erkrankung mit hoher Wahrscheinlichkeit vermuten? Was versprechen wir uns überhaupt von weiteren Untersuchungen? Eigentlich erwarten wir, dass weitere Untersuchungen die Vortestwahrscheinlichkeit relevant verändern, wie in der Abbildung 21-1 dargestellt. Wenn wir von einer bestimmten Vortestwahrscheinlichkeit ausgehen, dann erwarten wir von einem positiven Testergebnis eine relevante Verschiebung nach rechts und bei einem negativen Testergebnis einen deutlichen Rutsch nach links. Wir würden durch ein positives Ergebnis also deutlich bestärkt und durch ein negatives Ergebnis verunsichert, so dass wir unsere Diagnose in Frage stellen würden.

Wenn wir uns quasi festgelegt haben, dass der Patient im ersten Szenario an einer Blinddarmentzündung leidet, dann gehört er eigentlich sofort operiert. Warum sollten wir weitere Tests veranlassen, wenn wir uns bereits zu 95 Prozent sicher sind? Gibt es einen Test, der unsere Verdachtsdiagnose noch weiter bestätigen kann, vielleicht sogar auf 100 Prozent? Nein, es gibt keinen Test, der uns eine 100%ige Sicherheit geben würde. Patienten und Ärzte werden immer mit einer gewissen Unsicherheit leben müssen. Viele Patienten glauben zwar daran, dass es doch möglich sein müsse, alle Krankheiten sicher zu diagnostizieren, aber diese Hoffnung ist illusorisch. Dieser naive Glaube trifft sicherlich auf einige fortgeschrittene Krankheiten zu, die der erfahrene Arzt bereits von weitem erkennt, aber nicht für die überwiegende Mehrheit der Krankheiten.

Es ist auch kaum möglich, unsere Sicherheit von 95 Prozent weiter zu steigern, wie wir bald erkennen werden. In unserer Situation, wenn wir uns schon sehr sicher sind, gibt es eigentlich nur einen Grund, einen weiteren Test vorzunehmen: um die Operation zu vermeiden. Es müsste ein Test sein, der unsere 95prozentige Vortestwahrscheinlichkeit auf 50 Prozent senkt und uns damit so verunsichert, dass wir auch über andere Diagnosen nachdenken müssten.

Werfen wir einen kurzen Blick auf die Routine im Krankenhaus. Bei dem Verdacht auf eine Blinddarmentzündung wird immer das Blut untersucht und die weißen Blutkörperchen (Leukozyten) gezählt. Da wir uns bereits vor der Blutuntersuchung auf eine Blinddarmentzündung festgelegt haben, stellt sich die Frage, bei welchem Laborwert wir unsere Diagnose revidieren würden. Betrachten wir dazu die weißen Blutkörperchen. Wenn eine Erhöhung (Leukozytose) vorläge, dann weist das auf eine Entzündung hin. Wir würden uns dann zwar bestätigt fühlen, aber die Untersuchung wäre pragmatisch nicht hilfreich gewesen, sondern eher überflüssig, weil wir ja schon vorher wussten, dass eine Entzündung vorliegt. Wie sähe es bei normalen oder erniedrigten Werten aus? Bei solchen Werten würden wir ebenfalls bei unserer Diagnose bleiben, weil sie Zeichen einer fortgeschrittenen Entzündung sein können. Egal, welche Ergebnisse wir aus der Blutuntersuchung der weißen Blutkörperchen erhalten, wir bleiben bei unserer Verdachtsdiagnose. Sollte jemand jetzt die logischen Konsequenzen erkennen, dann könnte er die Ärzte fragen, warum sie in solchen Situationen überhaupt diese Blutuntersuchung vornehmen. Wahrscheinlich werden wir darauf keine vernünftige Antwort hören, sondern lediglich „das haben wir schon immer so gemacht“.

Der tatsächliche Einfluss des Ergebnisses auf die bereits getroffene Entscheidung wird im ärztlichen Alltag viel zu wenig beachtet. Eigentlich sollten wir jede angeordnete Untersuchung daraufhin hinterfragen, ob die Ergebnisse, egal wie sie ausfallen, überhaupt einen Einfluss auf das weitere Vorgehen haben können. Wenn das nicht der Fall ist, dann sollten wir die Notwendigkeit für die Untersuchung sehr kritisch betrachten. Wir könnten dadurch nicht nur Kosten sparen, sondern wir vermeiden dadurch auch die falsch-negativen und falsch-positiven Ergebnisse und ihre Konsequenzen. Mit solchen überflüssigen Untersuchungen befriedigen wir noch nicht einmal unsere akademische Neugierde, denn sie vermitteln uns keine relevanten neuen Informationen.

In unserem ersten Szenario mit einem eindeutigen Befund und einer relativ sicherer Diagnose ist es eher unwahrscheinlich, dass wir unsere Meinung ändern werden. Wir könnten natürlich eine Ultraschalluntersuchung oder Computertomographie veranlassen. Auch hier müssen wir uns fragen, bei welchen negativen Befunden uns die Untersuchungen von einer Operation abhalten würden? Wie bereits betont, interessieren nicht die positiven Befunde, denn es dürfte doch unwesentlich sein, ob meine Sicherheit 95 oder 99 Prozent beträgt – operiert werden muss der Patient sowieso.

Im zweiten Szenario sind wir von Beginn an unsicher. Hier würden wir uns wünschen, dass weitere Untersuchungen unsere angenommene Vortestwahrscheinlichkeit von 40 Prozent entweder auf zehn Prozent oder auf 80 Prozent verändern, so dass wir uns eindeutig für eine abwartende oder operative Therapie entscheiden können. Ob wir weitere Untersuchungen veranlassen, hängt also wesentlich damit zusammen, ob wir einen deutlichen Unterschied nach dem Test erwarten. Die sogenannte Nachtestwahrscheinlichkeit sollte sich von der Vortestwahrscheinlichkeit deutlich, relevant oder signifikant unterscheiden. Wenn wir nach dem Test dieselbe Wahrscheinlichkeit generieren wie vor dem Test, dann wäre der Test nicht hilfreich. Er mag, wie bereits betont, akademisch interessant sein, aber er ist pragmatisch nutzlos.

Fassen wir noch einmal zusammen. Nachdem wir alle verfügbaren Informationen gesammelt und uns orientiert haben, ob ein bestimmter Zustand oder eine bestimmte Krankheit vorliegen könnte, schätzen wir die Wahrscheinlichkeit, dass der Zustand oder die Krankheit besteht. Wir würden nur dann weitere Informationen einholen oder weitere Tests durchführen, wenn wir uns davon eine Veränderung der Vortestwahrscheinlichkeit versprechen.

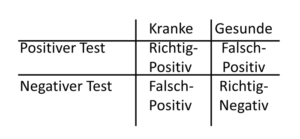
Tab. 21-1   Mögliche Testergebnisse bei Kranken und Gesunden

Nachdem wir nun wissen, was wir mit der Vortestwahrscheinlichkeit bewerkstelligen sollen, blicken wir erwartungsvoll auf die Tür, die uns in den nächsten Raum führen soll. Die Tür ist beschriftet mit „Likelihood Ratio“ (LR). In der englischen Sprache wird zwar zwischen „probability“ und „likelihood“ unterschieden, aber beide Begriffe werden hier einfach mit „Wahrscheinlichkeit“ übersetzt. „Ratio“ können wir mit „Verhältnis“ oder „Quotient“ übersetzen. Wir sprechen also über Wahrscheinlichkeitsverhältnisse. Genau genommen gelten diese Verhältnisse immer nur für ein positives oder negatives Testergebnis. Man spricht also genauer über die Likelihood Ratio des positiven Tests (LR+) oder des negativen Tests (LR–).

Wir dürfen uns auch dieses Mal nicht von diesen Begriffen abschrecken lassen. Mittlerweile haben wir doch gelernt, dass hinter diesen Fachbegriffen immer relativ einfache Konstruktionen stehen. So ist es auch hier. Wenn wir die nächsten Absätze nachvollzogen haben, werden wir für alles Weitere gut gerüstet sein. Betrachten wir zunächst die Tabelle 23-1, die wir bereits von früher kennen. Hier werden die Kranken und Gesunden mit den Testergebnissen in Beziehung gesetzt. Günstig wäre zweifelsfrei, wenn wir nur richtig-positive und richtig-negative Ergebnisse hätten, aber das ist leider so gut wie nie der Fall. Wir hatten gelernt, dass wir aus der Tabelle die Sensitivität und Spezifität berechnen können, indem wir entweder auf die Kranken oder auf die Gesunden schauen. Wir hatten aber auch gesehen, dass uns das im ärztlichen Alltag wenig hilft, weil wir ja nicht wissen, ob der Patient tatsächlich krank ist. De facto werden wir mit einem positiven oder negativen Testergebnis konfrontiert und müssen daraus auf die Krankheit schließen. Hier helfen uns eigentlich nur die Vorhersagewerte, die sich aber ändern, weil sie von der Prävalenz/Vortestwahrscheinlichkeit abhängen. Soweit, so gut. Diese Zusammenhänge haben wir bisher diskutiert und sicherlich auch verstanden. Aber was soll nun noch die LR?

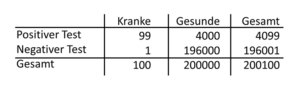
Tab. 21-2   Lungenkrebs bei der zweiten Untersuchung unseres Neffen

Was ist dieses Wahrscheinlichkeitsverhältnis, die Likelihood Ratio? Wie unterscheidet sie sich von den anderen Begriffen? Betrachten wir dazu zunächst noch einmal Tabelle 21-2. Aus der Zeile mit den positiven Untersuchungsergebnissen haben wir den Vorhersagewert berechnet. Er betrug 99/4.099. Die LR+ berechnet sich nicht aus den absoluten Zahlen wie der Vorhersagewert, sondern aus Anteilen. Sie ist ein Verhältnis zwischen zwei Anteilen, die wir berechnen müssen. Der erste Anteil ist der der positiv-getesteten Kranken an den Kranken (99/100). Er entspricht somit der Sensitivität und lässt sich in der Spalte der Kranken ablesen. Der zweite Anteil ist der der positiv-getesteten Gesunden an den Gesunden (4.000/196.000). Er entspricht somit (1-Spezifität) und kann aus der Spalte der Gesunden abgelesen werden. Das Verhältnis zwischen beiden „Sensitivität:(1-Spezifität)“ ist die gesuchte LR+.

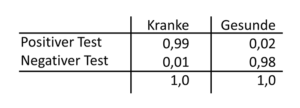
Tab. 21-3   Lungenkrebs bei der zweiten Untersuchung unseres Neffen

Das mag alle sehr kompliziert klingen, aber es ist sehr wichtig, dass wir den Sinn der LR begreifen. Deshalb werden wir die Tabelle 21-2 so verändern, dass in ihnen nur noch die Anteile der Spalten stehen. Wir erkennen jetzt aus der Tabelle 21-3 auf einen Blick, dass die Prävalenz keine Rolle mehr spielt, weil die Anteile entlang der Spalten wie die Sensitivität und Spezifität berechnet wurden. Die LR+ beträgt demnach 0,99:0,02=49,5.

Ähnlich verhält es sich natürlich auch bei einem negativen Testergebnis. Betrachten wir noch einmal die Tabelle 21-3. Hier setzen wir dem Anteil der Falsch-negativen an den Kranken (1/100) ins Verhältnis zu dem Anteil der Richtig-negativen an den Gesunden (98/100). Der erste Anteil entspricht (1-Sensitivität) und der zweite Anteil entspricht der Spezifität. Die Likelihood Ratio für einen negative Test (LR-) berechnet sich demnach aus dem Quotienten „(1-Sensitivität):Spezifität“. Für ein negatives Ergebnis beträgt die LR- 0,1:0,98=0,01.

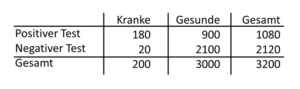
Tab. 21-4   Übung

Üben wir das an einem anderen Beispiel aus der Tabelle 21-4. Wie hoch ist die LR+? Dazu müssen wir für die 180 richtig-positiven Patienten berechnen, wie hoch der Anteil an den Kranken ist. Er beträgt 180/200, also 0,9. Die 900 falsch-positiven Gesunden entsprechen 900/3000, also 0,3. Die LR+ beträgt somit 0,9:0,3=3. Die LR- beträgt dagegen 0,1:0,7=0,14.

Die Größe der Likelihood Ratio lässt uns abschätzen, wie viel Mal häufiger eine Erkrankung vorliegt oder nicht, wenn das Ergebnis positiv oder negativ ist. In der Tabelle 21-5 ist zusammengestellt, wie wertvoll eine Untersuchung sein kann, wenn wir allein die LR betrachten. Ist die LR über zehn oder unter 0,1 dann ist der Test sicherlich sehr hilfreich. Ist die LR dagegen zwischen 0,5 und 2, dann sollten wir ernsthaft überlegen, ob wir nicht auf den Test verzichten.

Jetzt sind wir bestens ausgerüstet, um auf den nächsten wissenschaftlichen Kongressen während des Vortrages über eine diagnostische Methode, die LR auszurechnen. Wir können dann sofort über die Sinnhaftigkeit des Testes entscheiden. Wird dort von einer Sensitivität von 80 Prozent bei einer Spezifität von 60 Prozent gesprochen, dann beträgt die LR+ nur 0,8:0,4=2. Wird die Sensitivität mit 90 Prozent und die Spezifität mit 70 Prozent angegeben, dann beträgt die LR+ immerhin 0,9:0,3=3, was immer noch nicht berauschend ist. Würde jemand entweder nur die Sensitivität oder nur die Spezifität angeben, dann könnten wir die LR nicht ausrechnen. Das wäre aber nicht unser Fehler, sondern der Vortragende wird etwas zu verheimlichen haben. Wir hatten bereits vorher gesehen, wie wir diese Gütekriterien manipulieren können, wenn wir nur ein Kriterium angeben.

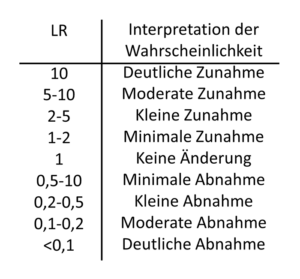
Tab. 21-5   Veränderung der Wahrscheinlichkeit einer Erkrankung in Abhängigkeit
von der Größe der Likelihood Ratio

Betrachten wir ein anderes medizinisches Szenario, um zu demonstrieren, wie nützlich die LR in Situationen ist, wo wir die Sensitivität und Spezifität nicht sofort zur Hand haben. Wir vermuten bei einem Patienten mit plötzlicher Luftnot nach einer Operation eine Lungenembolie, d.h. hier hat sich ein Blutgerinnsel festgesetzt, das zu einer lebensbedrohlichen Luftnot führen kann. Um die Diagnose zu sichern, veranlassen wir eine Computertomographie. Der Radiologe ruft uns an und teilt uns mit, dass es nicht ganz sicher ist, dass der Patient eine Lungenembolie hat. Er hält sie nur für wahrscheinlich. Was schließen wir daraus? Um aus dieser radiologischen Aussage Konsequenzen abzuleiten, müssten wir wissen, wie gut die Computertomographie zur Diagnose der Lungenembolie beiträgt. Wir führen eine Literaturrecherche durch und stoßen dabei auf eine aktuelle Untersuchung zu diesem Thema mit der Tabelle 21-6.

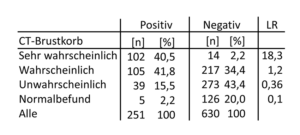
Tab. 21-6   Untersuchungsergebnisse der Computertomographie bei Lungenembolien

Offensichtlich können wir hier nicht direkt die Begriffe der Sensitivität und Spezifität anwenden, denn die sind nur für einfache Testverfahren definiert. Deshalb wählen wir ein einfaches alternatives Vorgehen, dass auf dem Konzept der LR beruht. Wir untersuchen die Tabelle zeilenweise daraufhin, wie gut die Computertomographie bei den verschiedenen Differenzierungen zwischen krank und gesund unterscheiden kann. Wir suchen die Likelihood-Ratio für jede einzelne Zeile. Wir setzen in jeder Zeile die einzelnen Anteile ins Verhältnis. In der obersten Zeile erhalten wir 40,5 Prozent der richtig-positiven Kranken zu 2,3 Prozent der falsch-positiven Gesunden. Hier beträgt die LR+ 18,3.

Ein sehr gutes Ergebnis. In der zweiten Zeile sind die Ergebnisse für die Aussage „wahrscheinlich“ aufgelistet, die uns interessieren. Hier stehen 41,8 Prozent der Kranken 34,4 Prozent der Gesunden gegenüber mit einer LR+ von 1,2. Damit ist die Aussage „wahrscheinlich“ für uns pragmatisch unbrauchbar. Ebenso verhält es sich mit „unwahrscheinlich“, weil hier die LR nur 0,36 beträgt. Hätte der Radiologe den Befund „normal“ erhoben, dann wäre uns wieder geholfen, weil damit eine LR von 0,1 verbunden ist. Wie wir an diesem Beispiel erkennen, ist nicht jede Untersuchung auch überall gleich aussagekräftig, wenn sie mehrere Klassifizierungen zulässt.

Da es nun langsam langweilig in diesem Raum wird, öffnen wir die dritte Tür mit der Aufschrift „Nachtestwahrscheinlichkeit“. So richtig neugierig sind wir jetzt nicht mehr und müde sind wir auch. Nachdem wir uns mit der Vortestwahrscheinlichkeit vertraut gemacht haben und wissen, wie wir die LR berechnen, können wir uns nun der Berechnung der Nachtestwahrscheinlichkeit zuwenden.

Abb. 21-2   Fagan-Nomogramm

Dafür sind verschiedene Formeln verfügbar, die wir glücklicherweise alle ignorieren dürfen. Einfacher ist nämlich der Gebrauch eines Nomogramms, das Fagan bereits 1975 publizierte [Fagan TJ. N Engl J Med 1975;293:2571]. Solch ein Fagan-Nomogramm ist in Abbildung 21-2 dargestellt. Hier suchen wir die Vortestwahrscheinlichkeit auf der linken Seite und die LR in der Mitte auf. Durch beide Punkte ziehen wir eine Gerade, die dann die Nachtestwahrscheinlichkeit auf der rechten Seite schneidet. Wenn wir damit ein wenig üben, dann werden wir schnell die Aussagekraft der Abbildung 23-2 erkennen. Wenn wir nämlich eine LR verwenden, die zwischen 0,5-2 liegt, dann ist das Testverfahren kaum hilfreich. Wir sollten deshalb immer Testverfahren anwenden, die eine sehr hohe oder sehr geringe LR aufweisen.

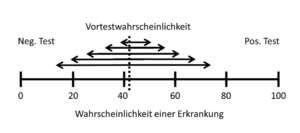
Abb. 21-3   Ändern der Vortestwahrscheinlichkeit bei unterschiedlichen LRs

Welche Konsequenzen ziehen wir aus dem Vorhergehenden? Wenn wir uns unsicher sind (Abb. 21-3), dann benötigen wir stark diskriminierende Testverfahren mit einer hohen oder niedrigen LR, damit sich die Nachtestwahrscheinlichkeit relevant verändert. Untersuchungsverfahren mit einer LR um 1 sind überhaupt nicht hilfreich und verschieben unsere Vortestwahrscheinlichkeit kaum. In den meisten Situationen können wir auf sie verzichten. Mit den leicht zu berechnenden LR haben wir somit ein Instrument, um die grundsätzliche Bedeutung des Testes beurteilen zu können.