Fallzahlberechnung
(Für Fortgeschrittene)
12. Fallzahlberechnung
Auf dem Korridor der induktiven Statistik schlendernd, fällt uns eine seltsam bemalte Tür auf, auf der in Großbuchstaben und leuchtender roter Farbe steht: „Fallzahlberechnung“. In diesem Raum sollen wir wohl mit etwas besonders Wichtigem vertraut gemacht werden.
Ohne Zweifel gehört die Fallzahlberechnung vor Beginn einer Studie zu den wichtigen und notwendigen Elementen einer guten Studie. Wir würden heute eine Studie ohne adäquate Fallzahlberechnung nicht mehr akzeptieren. Warum das so ist, werden wir gleich sehen. Gefordert werden aber nicht nur eine Fallzahlberechnung, sondern eine adäquate Fallzahlberechnung. Diesen Unterschied werden wir auch bald verstehen.
Was bezwecken wir mit einer Fallzahlberechnung? Mit dieser Berechnung legen wir fest, wie viele Personen in die Studie aufgenommen werden (müssen). Warum müssen wir die Fallzahl überhaupt festlegen? Diese Frage können wir leicht beantworten, wenn wir uns an die Ausführungen des vorigen Kapitels erinnern. Durch eine beliebige Erhöhung der Stichprobe wird immer ein signifikantes Ergebnis erreichbar. Wenn wir eine Stichprobe ausreichend groß wählen, können wir quasi jede These belegen. Warum ist das schlimm? Weil dadurch möglicherweise Personen oder Gesellschaften geschädigt werden. Hier werden wahrscheinlich einige stutzen. Warum sollte jemand geschädigt werden? Stellen wir uns vor, wir vergleichen zwei blutdrucksenkende Medikamente A und B. Das neue Medikament B ist doppelt so teuer wie A. In einer vergleichenden Untersuchung an 5000 Patienten senkt das teure Medikament den Blutdruck signifikant besser (p=0,01), und zwar um 2 mmHg bei einer Standardabweichung von 20 mmHg. Wir würden unser Gesundheitssystem schädigen, wenn wir für diesen Unterschied von 2 mmHg, der klinisch nicht relevant ist, unsere Ressourcen verschwenden. Natürlich könnten wir hier einwenden, dass das Beispiel doch sehr weit konstruiert wurde. Ja, das ist richtig und auch beabsichtigt. Solche Studien, die nicht relevante Vorteile offenbaren und dabei die Kosten deutlich erhöhen, sind leider sehr häufig. Im medizinischen Bereich sind es typischerweise die Pharmaindustrie und die Instrumentenhersteller, die aus verständlichen und nachvollziehbaren ökonomischen Interessen neue Produkte auf den Markt bringen, deren Kosten in einem sehr schlechten Verhältnis zum zusätzlichen Nutzen stehen. Hier werden von der Industrie keine Kosten gescheut, um durch sorgfältig geplante, aber schlechte Studien einen pseudowissenschaftlichen Nachweis darüber zu erbringen, dass der zusätzliche Nutzen überwiegt.

Betrachten wir ein anderes Beispiel: In einer Studie werden zwei Operationsverfahren verglichen. Das herkömmliche Verfahren führt innerhalb von sechs Monaten bei 25 Prozent der Patienten zu Rückfällen, während das neue deutlich besser sein soll. Wir führen keine Fallzahlberechnung durch und nehmen 1000 Patienten in die Studie auf. Nach vier Jahren ist diese Studie abgeschlossen und offenbart, dass die Rückfallrate des neuen Verfahrens bei neun Prozent liegt. Haben wir mit der Studie jemand geschädigt? Ja, sogar sehr viele. Wenn wir vorher eine Fallzahlberechnung durchgeführt hätten, hätten wir diese Studie wahrscheinlich schon nach 200 Patienten beenden können. Dann hätten wir gewusst, dass die neue Methode besser ist. Das wäre korrekt gewesen. Stattdessen haben wir auf die Fallzahl verzichtet und 800 Patienten überflüssigerweise in die Studie aufgenommen. Davon wurden 400 Patienten nach der neuen Methode operiert. Diese Patienten wurden nicht geschädigt. Aber die anderen 400 Patienten wurden nach der alten und schlechteren Methode operiert und damit geschädigt. De facto haben wir 64 Rückfälle verursacht, die unnötig gewesen wären. Neben dem moralischen Problem, dass wir einigen Patienten das bessere Verfahren vorenthalten und sie damit schlechter behandeln, als nötig gewesen wäre, verschwenden wir auch Studienressourcen, indem eine zu hohe Fallzahl wählen.
Bisher haben wir zwei Beispiele angeführt, in denen zu viele Patienten in Studien aufgenommen wurden. Viel, viel häufiger sind aber Studien, in denen zu wenig Patienten aufgenommen wurden. Der Zweck einer kleinen Studienpopulation ist evident. Die Studie ist deutlich preiswerter und schneller durchführbar. Die gewünschten Ergebnisse liegen schneller vor und in einigen Fällen sind die Erkrankungen so selten, dass eine größere Studie nicht realisierbar ist. Wir könnten hier auf die Idee kommen, dass es besser ist, eine schlechte Studie durchzuführen als gar keine Studie, um zumindest einige Informationen generieren. Das ist aber völlig falsch. „Faule“ Ergebnisse könnten uns nicht nur in die Irre führen, sondern auch weitere wichtige Forschungen blockieren, weil wir potentiell bessere Alternativen ausschließen. Und wenn sich die „falschen“ Ergebnisse aus „faulen“ Studien erst einmal in das Gedächtnis der Bevölkerung eingeprägt haben, dann ist es ganz schwierig, die Zusammenhänge richtig zu stellen oder neue Studien gegen die „falschen“ Ansichten durchzuführen.
Mit jeder wissenschaftlichen Studie wird suggeriert, dass sie sorgfältig geplant und durchgeführt wurde und ihre Ergebnisse einwandfrei und unanfechtbar erhoben wurden. Erst dadurch werden die Ergebnisse ernsthaft verwertbar und erhalten ihr wissenschaftliches Qualitätsmerkmal. Alles das würde bei einer schlechten Studie aber nicht zutreffen, so dass wir die Ergebnisse nicht sinnvoll interpretieren können. Es ist deshalb immer besser, nach anderen Lösungen zu suchen, als eine schlechte Studie durchzuführen und die Ressourcen zu verschleudern.

Zu kleine Studienpopulationen führen sehr häufig zum ß-Fehler, den wir eigentlich so gering wie möglich halten wollten. Wir können ihn nicht in derselben Weise kontrollieren wie den α-Fehler, weil wir nicht wissen, welches Ergebnis wir in der Vergleichsgruppe erwarten können. Wir wollen aber mindestens sicherstellen, dass sich tatsächliche und bedeutsame Unterschiede als signifikant erweisen, so dass wir uns auch richtigerweise für die Alternativhypothese entscheiden. Ob eine Studie auch die nötige Teststärke hat, die nötige Power, um einen Unterschied als signifikant zu erweisen, können und sollten wir vorher berechnen. Dazu führen wir die Fallzahlberechnung durch. Wir wollen weder zu viele Patienten noch zu wenige Patienten in die Studie aufnehmen.
Jetzt wollen wir die Fallzahl für eine konstruiert Studie berechnen. In diesem Beispiel wollen wir durch den Einsatz neuer Instrumente die Operationszeit verkürzen. Wir vergleichen die Operationszeiten zweier Operationsverfahren N und A. In der Gruppe N werden die neuen Instrumente verwendet und in der Gruppe A die herkömmlichen Instrumente. Als ersten Schritt suchen wir in der Literatur nach der durchschnittlichen Operationszeit der alten Operationsmethode A. Sie beträgt 130±30 Minuten. Im zweiten Schritt legen wir fest, welchen Unterschied wir für klinisch relevant halten. Wir wissen aus unseren früheren Überlegungen, dass die Stichprobengröße zunehmen muss, wenn wir kleine Unterschiede beweisen wollen. Wir wissen auch, dass die teuren neuen Instrumente nur dann ökonomisch einsetzbar sind, wenn sie die Operationszeit um mindestens 15 Minuten verkürzen. Deshalb legen wir fest, dass wir einen Unterschied von 15 Minuten als signifikant nachweisen wollen. Wird der Unterschied größer als 15 Minuten ist es dann umso besser. Der α-Fehler wird auf fünf Prozent festgesetzt (α=0,05) und der ß-Fehler auf zwanzig Prozent (ß=0,2). Diese Fehlergrenzen sind allgemein akzeptiert und wir sollten immer dann, wenn wir von ihnen abweichen, gute und nachvollziehbare Gründe angeben. Um die erforderliche Fallzahl zu berechnen, müssen wir jetzt nur noch die Standardabweichung angeben, die gemäß der Literatur 30 Minuten beträgt.

Fassen wir zusammen, was wir für eine Fallzahlberechnung benötigen, wenn wir numerische Werte vergleichen wollen. Wir legen den α-Fehler auf 0,05 fest. Wir entscheiden uns bei einem p-Wert von unter 0,05 zugunsten der Alternativhypothese und gehen dabei das Risiko von fünf Prozent ein, dass wir uns irren. Wir legen den ß-Fehler auf 0,2 fest. Wir akzeptieren, dass wir zu 20 Prozent den vermuteten Unterschied nicht nachweisen können. Unter 1-ß verstehen wir die so genannte Teststärke oder Power der Studie. Sie beträgt 80 Prozent, d.h. mit 80%iger Wahrscheinlichkeit können wir den Unterschied nachweisen, wenn er vorliegt. Die Teststärke wird allgemein auf 80 Prozent festgesetzt. Wir könnten sie erhöhen, indem wir die Fallzahl erhöhen.
Wir benötigen weiterhin eine klare Angabe, welchen genauen Unterschied wir in der Studie nachweisen wollen. Wir müssen festlegen, welcher Unterschied für uns von Bedeutung ist. Als letzte Angabe benötigen wir ein Maß für die Streuung der Daten. Dazu suchen wir aus der Literatur vergleichbare Studien heraus und entnehmen aus ihnen die Standardabweichung. Verfügen wir über keinerlei Informationen zur voraussichtlichen Streuung, können wir darüber nur Vermutungen anstellen, so dass unsere Berechnung deutlich fehlerbehaftet sein wird. Im Laufe der Studie sollte die Fallzahl im Rahmen einer Zwischenauswertung neu berechnet werden, indem die Studienergebnisse bei der Berechnung berücksichtigt werden.

Tab. 12-1 Fallzahl verschiedener Unterschiede D für eine Standardabweichung von 30 Min.
Mit diesen vier Angaben füttern wir jetzt ein Computerprogramm wie z.B. „Power and Sample Size Calculation“, das kostenlos aus dem Internet heruntergeladen werden kann. Nachdem wir alle erforderlichen Daten eingetragen haben (Abb. 12-1), wird die Fallzahl berechnet. Danach beträgt die Fallzahl 64 Patienten pro Gruppe, also 128 für die gesamte Studie.
Wir sollten mit diesem Programm etwas „spielen“, um eine Gefühl für die Fallzahlberechnung zu bekommen. Wir lassen zunächst α, ß und die Standardabweichung von 30 Minuten unberührt und ändern nur den Unterschied zwischen den Gruppen, den wir als signifikant nachweisen wollen. Das Ergebnis ist in Tabelle 12-1 abgebildet. Danach sinkt die erforderliche Fallzahl, wenn wir größere Unterschiede suchen, und es steigt die Fallzahl, wenn wir den Unterschied zwischen den Gruppen verringern. Das haben wir auch so erwartet, weil es immer schwieriger wird, kleinere Unterschiede als signifikant nachzuweisen.
Diese Tabelle könnte auch den einen oder anderen Untersucher verführen. Verführen wozu, werden sich einige fragen? Dazu, dass man die Fallzahlberechnung „modelliert“. Dabei geht man so vor, dass zunächst geschätzt wird, wie viele Patienten man realistisch in dem veranschlagten Zeitraum rekrutieren kann. In einem zweiten Schritt wird dann mit dem Computerprogramm überprüft, welchen Unterschied man mit der Fallzahl nachweisen kann. In einem dritten Schritt wird dann genau dieser Unterschied als relevant beschrieben. Hierbei wird demnach die übliche Reihenfolge vertauscht. Es wird nicht zuerst die Fallzahl berechnet, sondern die Fallzahl wird vorgegeben und dann wird berechnet, welchen Unterschied wir mit dieser Fallzahl noch als signifikant nachweisen können. Dieser Vorgang ist zunächst völlig unproblematisch, weil wir ja auch feststellen möchten, welchen Unterschied wir mit der verfügbaren Fallzahl feststellen können. Sollte die Fallzahl nicht ausreichen, dann könnten wir immer noch versuchen, mehr Patienten zu rekrutieren, indem wir mehr Studienzentren integrieren. Problematisch wird dieser Ansatz erst, wenn wir einen unrealistischen Unterschied zwischen den Gruppen wählen, um der Fallzahlberechnung zu genügen. Wenn wir zum Beispiel nur wenige Patienten für die Studie rekrutieren können, dann können wir auch nur große Unterschiede als signifikant nachweisen. Der Untersucher könnte jetzt durch „geschickte“ Literaturselektion behaupten, dass dieser Unterschied eintreten wird. Damit hat er sich aber einen Bärendienst erwiesen. Wenn der Unterschied nämlich kleiner ausfällt, dann wird er aufgrund der niedrigen Fallzahl nicht mehr signifikant. Deshalb sollten wir bei jeder Fallzahlberechnung kritisch prüfen, ob der angepriesene und zu Grunde gelegte Unterschied tatsächlich sinnvoll ist oder nicht.
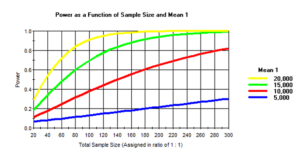
Abb. 12-2 Fallzahlberechnung für vier Unterschiede und einer Standardabweichung von 30 Minuten
Mit dem kostenlosen Computerprogramm lassen sich auch Abbildungen erstellen, die für mehrere Unterschiede abbilden, mit wie vielen Patienten wir welche Teststärke erreichen können. Die Abbildung 12-2 zeigt vier Kurven für die Unterschiede von fünf bis 20 Minuten. Für jeden Unterschied können wir jetzt ablesen, wie viele Patienten wir für eine Teststärke von 80 Prozent benötigen würden. Um einen Unterschied von fünf Minuten nachzuweisen, müssten wir extrem viele Patienten in die Studie aufnehmen. Selbst wenn wir 300 Patienten rekrutieren, würden wir nur eine Teststärke von 30 Prozent erreichen. Der ß-Fehler wäre 70 Prozent, d.h. wir würden solche Unterschiede kaum mit dieser Fallzahl nachweisen können. Wenn dagegen ein größerer Unterschied von 10 mmHg vermutet wird, dann beträgt die Teststärke mit 300 Patienten bereits 80 Prozent. Wenn wir einen Unterschied von 15 mmHg belegen wollen, dann benötigen wir für dieselbe Teststärke von 80 Prozent nur noch 120 Patienten und bei einer Differenz von 20 mmHg sogar nur noch nach 70 Patienten in jeder Gruppe.

Tab. 12-2 Fallzahl verschiedener Standardabweichungen (SD) für einen Unterschied von 20 Min.
Bei unserer nächsten Simulation werden wir den Unterschied zwischen den Gruppen gleich groß belassen, aber dafür die Streubreiten verändern. Die Ergebnisse in Tabelle 12-2 entsprechen unseren Erwartungen. Je größer die Streubreite bzw. Standardabweichung, umso unsicherer werden die Studienergebnisse und umso mehr Patienten müssen in die Studie eingeschlossen werden, um dieselbe Teststärke zu bewahren.
Der Einfluss der Streubreite ist aber nicht so eindrucksvoll wie die Änderung der Unterschiede zwischen den Gruppen, wie wir in der Abbildung 12-3 ablesen können. Mit zunehmender Streubreite werden die Kurven flacher und wir benötigen mehr Patienten, um unserer angestrebte Teststärke von 80 Prozent auch zu erreichen. Auch hier besteht die Möglichkeit der „modulierten“ Fallzahlberechnung. Wir suchen uns die Streubreite, die wir uns „leisten“ können und durchforsten dann solange die Literatur, bis wir „nachweisen“ können, dass das die zu erwartende Standardabweichung ist.
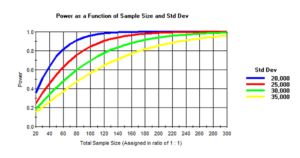
Abb. 12-3 Fallzahlberechnung verschiedener Standardabweichungen (SD) für einen Unterschied von 20 Min.
Wir haben in unseren Beispielen weder den α-Fehler noch den ß-Fehler verändert. Natürlich beeinflussen auch diese Werte die Fallzahl. Aber wir sollten schon sehr gute Gründe anführen, um diese Werte zu ändern. Mit dem Computerprogramm ist es leicht, die Änderungen der Fallzahl zu simulieren, und es sind alle aufgefordert, sich damit vertraut zu machen.
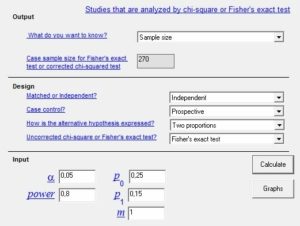
Abb. 12-4 Fallzahlberechnung
von Häufigkeiten
Wir wollen in einem anderen Beispiel auch den Umgang mit Häufigkeiten lernen (Abb. 12-4). Stellen wir uns vor, wir haben einen neuen beschichten Katheter entwickelt, der die Infektionsrate bei Intensivpatienten drastisch mindern soll. Wir konzipieren eine randomisierte Studie und nehmen als Hauptzielkriterium die Infektionen durch den Katheter mit eindeutigem Nachweis von Bakterien am Katheter. Es sollen nur Patienten eingeschlossen werden, bei denen der Katheter mindestens zehn Tage verwendet wird. Den α- und ß-Fehler lassen wir auf den Standardeinstellungen. Wir vermuten eine Katheterinfektion in fünf Prozent der Patienten und wollen einen Unterschied von zwei Prozent nachweisen. Dieses Mal geben wir die Daten wieder in dasselbe Computerprogramm ein. Allerdings nicht unter „t-Test“, sondern unter „Dichotomous“, weil wir ja die beiden Ergebnisse „ja“ oder „nein“ untersuchen. Wir erhalten als Ergebnis 3208 Patienten. Nach einem ersten Schock, denn so viele Patienten werden wir niemals für solch einer Studie gewinnen können, „modulieren“ wir auch diese Konstellation. Wenn wir die Rate an Katheterinfektionen auf sechs Prozent erhöhen und einfach behaupten, dass wir die Infekte auf zwei Prozent reduzieren, dann benötigen wir nur noch 850 Patienten. Das erscheint immer noch zu viel. Also erhöhen wir die Infektionsrate der herkömmlichen Katheter auf zehn Prozent und die der neuen auf drei Prozent. Dann bräuchten wir nur noch 444 Patienten. Das sind immer noch sehr viele Patienten, aber in einer multizentrischen Studie machbar. – Sinnvoll ist dieses Vorgehen aber nicht! Wir haben hier solange simuliert, bis wir eine geeignete Fallzahl ermittelt haben. Wenn wir die Studie durchführen und die dann nachgewiesenen Katheterinfektionen betragen nur fünf Prozent, wie zu Beginn angenommen, dann wird der Signifikanztest definitiv NICHT positiv. Wir haben uns erneut einen „Bärendienst“ erwiesen. Wir haben mit unserer „manipulierten“ Fallzahlberechnung eine von vornherein zum Scheitern verurteilte Studie durchgeführt und damit viele Ressourcen verschleudert.
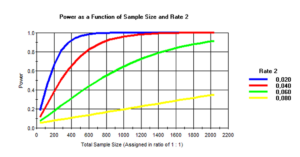
Abb. 12-5 Fallzahlberechnung für Häufigkeiten von zehn Prozent
Von vielen Forschern wird unterschätzt, wie schwierig es ist, kleine Unterschiede zu belegen. Wenn wir zum Beispiel die Rückfallrate einer Operation auf zehn Prozent schätzen und wir wollten einen Unterschied von zwei Prozent nachweisen, dann entspräche dass zwar einer relativen Reduktion von 20 Prozent, aber wir müssten die Fallzahl nach der Kurve in Abbildung 12-5 berechnen. Selbst wenn wir glauben, die Rückfallrate von zehn Prozent auf sechs Prozent zu senken, also um 40 Prozent, dann müssten wir unsere Berechnung einer anderen Kurve richten. Selbst gewaltige Verbesserungen sind durch Studien kaum zu belegen, wenn bereits die „Ausgangshäufigkeit“ relativ gering ist. Deshalb werden Studien über Komplikationen oder gar über die Sterblichkeit so gut wie nie signifikant. Und deshalb weichen viele Untersucher auf weniger relevante Parameter aus, um ihre neue Methode „wissenschaftlich“ abzusichern. In der Chirurgie wurden wahrscheinlich Hunderte von Millionen Euro von der Industrie gesponsert, um nachzuweisen, dass die minimal-invasive Chirurgie zu weniger postoperativen Schmerzen oder einem schnelleren Kostaufbau führt. Selten wurde überhaupt versucht, weniger Komplikationen oder eine geringere Sterblichkeit nachzuweisen. Es wurden gezielt Parameter gewählt, die zu signifikanten Unterschieden führten, um die neue und deutlich teurere Methode zu fördern. Allerdings waren diese Parameter bereits nach einigen Tagen nicht mehr von Relevanz.
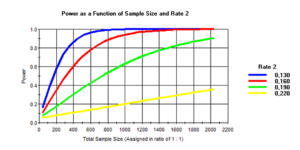
Abb. 12-6 Fallzahlberechnung
Wenden wir unsere Kenntnisse im folgenden Studiendesign an: In einer randomisierten Studie sollen die Raten an Narbenbrüchen überprüft werden. Mit einem neuen Fadenmaterial sollen die Narbenbrüche von durchschnittlich 25 Prozent auf 15 Prozent gesenkt werden. Für α=0,05 und ß=0,2 beträgt die Fallzahl 540, die wir in einer multizentrischen Studie rekrutieren wollen. Nur glaubt wirklich jemand, dass es mit einem neuen Faden gelingt, die Narbenbrüche um 40 Prozent zu senken? In der Abbildung 12-6 sind für verschiedene Unterschiede die Fallzahlen und Teststärken angeführt. Wenn wir uns auf eine Fallzahl von 540 beschränken würden und die absolute Reduktion nur drei oder sechs Prozent betragen würde, dann könnten wir sie nicht nachweisen. Deshalb noch einmal die Warnung vor dem Versuch, kleine Unterschiede bestätigen zu wollen.
Auch hier gäbe es die theoretische Möglichkeit, die Fallzahl zu reduzieren, indem wir die geschätzte Rate an Narbenbrüchen auf 30 Prozent oder sogar auf 35 Prozent „erhöhen“. Es gibt durchaus ausgewählte Literaturstellen, z.B. bei Patienten nach Aortenrupturen, die eine so hohe Rate an Narbenbrüchen belegen. Der „kreative“ Untersucher könnte also durch eine geschickte Auswahl der Literatur die höhere Rate an Narbenbrüchen begründen. Wir sollten deshalb genau darauf achten, welche Ausgangssituation unterstellt wird. Wenn die Ausgangslage als zu hoch oder zu niedrig erscheint, sollten wir die Fallzahlberechnung ernsthaft hinterfragen. Vielleicht waren dem Untersucher tatsächlich nur solche selektierten Literaturstellen mit zu hohen oder zu niedrigen Werten zugänglich und er hat nach bestem Wissen und Gewissen diese Werte festgelegt. Vielleicht, vielleicht aber auch nicht. Die Tatsache, dass eine Fallzahlberechnung vorliegt, bedeutet noch nicht, dass sie auch adäquat ist. Dieser Sachverhalt ist immer gesondert zu prüfen, und wenn uns dabei etwas auffällt, dann ist die gesamte Studie als äußerst suspekt zu bewerten. Wer bereits bei solch grundlegenden Ansprüchen „schummelt“, dem ist alles zuzutrauen.
Die Wahl einer „richtigen“ Stichprobengröße soll sicherstellen, dass wir einen Unterschied, wenn er tatsächlich vorliegt, auch als signifikant nachweisen können. Dazu ist die Studie gedacht. Die Berechnung der erforderlichen Fallzahl ist ein äußerst wichtiger und komplexer Prozess, indem nicht nur die wenigen Parameter eingehen, die wir bisher besprochen haben, sondern das gesamte Studiendesign. Es ist deshalb erforderlich, die Fallzahlberechnung gemeinsam mit einem Statistiker zu besprechen, und auszuloten, welche Studie mit welcher Fallzahl realistisch ist. Wir sollten unbedingt jede „Manipulation“ oder „Verschönerung“ der Berechnung unterlassen, weil wir sonst nach Studiendurchführung auf einen Scherbenhaufen blicken werden. Eine Studie ohne adäquate Fallzahlberechnung ist ein schwerer Qualitätsmangel und sollte immer dazu führen, dass wir den Studienergebnissen misstrauen.