Stichprobengröße
Bis jetzt hatten wir nur auf den α-Fehler geblickt. Selbstverständlich wollen wir auch wissen, wie wir den zweiten Fehler, den ß-Fehler beeinflussen können. Dieser Fehler kann eintreten, wenn wir in unserer Studie keinen signifikanten Unterschied finden und die Nullhypothese akzeptieren, obgleich ein tatsächlicher Unterschied besteht. Wie kann das überhaupt geschehen? Nehmen wir zwei Operationsverfahren, von denen behauptet wird, dass das Verfahren A deutlich schneller ist als das Verfahren B. Die verkürzte Operationszeit ist bedingt durch ein neues Instrument, das 500 € kostet. Bei diesen hohen Kosten wollen wir wissen, ob sich die Operationszeit tatsächlich verkürzt. Wir legen fest, dass zur Kostendeckung eine Verkürzung von 15 Minuten akzeptabel ist. Wir führen eine Studie durch und der Unterschied zwischen beiden Gruppen beträgt 20 Minuten. Wir jubeln bereits – gemeinsam mit dem Instrumentenhersteller -, weil das Instrument die Operation komfortabler gestaltet und es zugleich kosteneffektiv ist. Die Verwaltung des Krankenhauses ist aber nicht von der Überlegenheit überzeugt und verlangt einen Signifikanztest, der p=0,2 erbringt. Daraufhin verbietet die Verwaltung den Gebrauch des Instrumentes. Was ist hier geschehen? Warum haben wir den deutlichen Unterschied von 20 Minuten nicht statistisch sichern können? Warum haben wir uns für die Nullhypothese entscheiden müssen, dass kein Unterschied besteht, obwohl ein deutlicher Unterschied von 20 Minuten nachweisbar war?
Das Problem wollen wir an einem zweiten Beispiel vertiefen. Wir haben ein neues Medikament, das wir bei Patienten mit einer ausgeprägten Leberzirrhose einsetzen, die viele Krampfadern an der Speiseröhre entwickelt haben und bei denen ein hohes Risiko besteht, dass diese bluten. Das neue Medikament A soll den Druck in den Krampfadern deutlich senken und dadurch die Rate an Blutungen vermindern. In einer randomisierten Studie vergleichen wir das Medikament A gegen Placebo. Nach zwölf Monaten hatten in der Medikamentengruppe zehn Prozent geblutet und in der Placebogruppe 20 Prozent. Das Medikament hat das Blutungsrisiko damit halbiert. Auch hier freuen wir uns zu früh, wenn wir bereits aus dem nachgewiesenen Unterschied auch auf den Erfolg schließen. Denn hier beträgt der p-Wert des Signifikanztests 0,15. Wir entscheiden uns auch hier zwangsläufig für die Nullhypothese und setzen das Medikament nicht ein.
Wir hätten eigentlich erwartet, dass diese großen und klinisch bedeutsamen Unterschiede durch die Studien hinreichend belegt werden. Wir vermuten hier einen ß-Fehler, d.h. wir vermuten, dass ein tatsächlicher Unterschied besteht, obwohl der Unterschied im Test nicht signifikant wird. Worauf könnte der ß-Fehler beruhen? Warum werden diese großen Unterschiede nicht statistisch signifikant? Es liegt an zwei Faktoren, der Stichprobengröße und der Streuungsbreite der Daten. Wir wollen in diesem Abschnitt den Einfluss beider Faktoren auf den Signifikanztest begreifen.

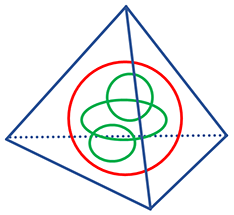
Abb. 11-1 Daten mit zunehmender Streubreite
Wir haben unsere Naivität bereits verloren, unterschiedliche Ergebnisse einfach so zu bewerten, als wenn sie einem tatsächlichen Unterschied entsprächen. Wir wissen bereits, dass Unterschiede als Schwankungen immer auftreten werden und bei der Beurteilung berücksichtigt werden müssen. Wenn wir ein und dieselbe Population wiederholt messen, dann erhalten wir nie exakt dieselben Resultate. Sie streuen zwangsläufig, mehr oder weniger. Wenn wir zwei Therapien miteinander vergleichen und die beiden Gruppenergebnisse unterscheiden sich nur gering, dann handelt es sich wahrscheinlich nur um eine „natürliche“ Variation ein und derselben Population und die Therapien unterscheiden sich nicht. Wenn dagegen die Unterschiede zwischen den Gruppen deutlich größer sind als die üblichen Streuungen, dann vermuten wir eher einen tatsächlichen Unterschied.
Diese Umschreibung wollen wir uns an einigen Graphiken verdeutlichen. Wir beginnen mit einfachen Box-Plots von Gruppen, die sich in ihrer Streuung deutlich unterscheiden. Woran können wir das erkennen? Indem wir auf die Verteilung der Daten achten, die durch die 95%-5%-Perzentilen gegeben sind. Zwischen diesen beiden Perzentilen befinden sich 90 Prozent aller Werte. Streuen die Werte sehr stark, dann sind die Perzentilen weit auseinander. Streuen sie nur gering, dann sind sie deutlich schmaler. Die Abbildung 11-1 zeigt bei demselben Medianwert eine zunehmende Varianz bzw. Streuungsbreite, die wir in der Regel als Standardabweichung der Werte angeben.
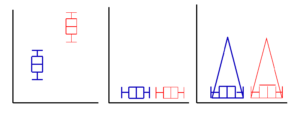
Abb. 11-2 Kippen der Box-Plots
Betrachten wir in der Abbildung 11-2 die Box-Plots einer blauen und roten Gruppierung. Die Box-Plots sind so gewählt, dass sie dieselbe Streuungsbreite haben. Die Medianwerte liegen sehr weit auseinander, so dass sich die beiden Gruppen deutlich unterscheiden. Jetzt nehmen wir den blauen und roten Box-Plot und drehen ihn um 90° im Uhrzeigersinn. Er liegt jetzt flach auf dem Boden. Wenn wir jetzt eine einfache und übersichtliche Idee der Verteilung der Daten wünschen, dann ziehen wir den Medianwert einfach in die Höhe, so dass ein gleichschenkeliges Dreieck entsteht. Die Basis des Dreiecks ist die 95%-5%-Perzentile der Box-Plots und die Höhe richten wir ein wenig willkürlich nach der Anzahl der Personen in den Studien aus. In unserem Beispiel sollen in beide Gruppen gleich viele Personen eingeschlossen sein, so dass die Dreiecke gleich hoch sind. Die Spitze des Dreiecks entspricht dem Median, so dass wir den Unterschied zwischen den Gruppen leicht erkennen können.
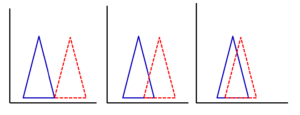
Abb. 11-3 Überlagern der Gruppen
Betrachten wir nun die Abbildung 11-2 genauer. Beide Dreiecke überlagern sich nicht und die Spitzen sind weit auseinander. Unsere beiden Box-Plots (blau und rot) unterscheiden sich bereits so deutlich, dass der signifikante Unterschied leicht erkannt werden kann. Anhand der Dreiecke gehen wir davon aus, dass wir uns zwei verschiedenen Populationen gegenüber sehen: der blauen Gruppe und der roten Gruppe. Was würden wir jetzt denken, wenn sich die Gruppen überlagern (Abbildung 11-3). Wenn sich die Dreiecke nur berühren, würden wir weiterhin behaupten wollen, dass es zwei verschiedene Populationen sind. Überlappen sie sich nur gering, beginnen unsere Zweifel und wenn sie sich sehr stark überlappen, dann sind wir uns fast sicher, dass es sich in Wirklichkeit nur um eine Population handelt und der nachgewiesene Unterschied ist nur zufällig entstanden.

Abb. 11-4 Eine einzige Gruppe oder zwei Gruppen
Was meinen wir damit, dass es sich nur um eine Population handelt, obgleich wir doch zwei Gruppen miteinander vergleichen? Wir dürfen nicht vergessen, dass wir zufällige Stichproben aus einer Grundgesamtheit gezogen haben, um eine Hypothese zu überprüfen. Dieses Auswählen einer Stichprobe könnten wir beliebig oft wiederholen. Wir würden erwarten, dass diese vielen Stichproben aus derselben Grundgesamtheit dennoch untereinander differieren und wir jedes Mal gering verschiedene Ergebnisse erhalten. Die Dreiecke würden sich alle sehr überlagern, aber auch ein wenig auseinander liegen. Allerdings würden wir auch erwarten, dass die Ergebnisse sich quasi um das „wirkliche“ Ergebnis verteilen, denn wir folgern später aus den vielen Einzelergebnissen auf das „wahre“ Ergebnis. Wenn wir zwei Gruppen miteinander vergleichen und einen tatsächlichen Unterschied erwarten, dann müssten sich die Stichproben voneinander so unterscheiden, als ob sie aus zwei verschiedenen Populationen gezogen worden wären. In der Abbildung 11-4 deuten wir unseren Glauben an, dass es sich zunehmend um eine Population handelt bzw. dass sich die Populationen nicht unterscheiden. Unser Glaube allein ist aber nicht ausreichend. Ob wir „richtig“ glauben, überprüfen wir besser durch einen Signifikanztest.
Welchen Einfluss hat nun die Streuungsbreite auf die Überlagerung? Ganz einfach. Je größer die Streuungsbreite, umso breiter ist die Basis des Dreiecks. Damit überlappen sich die Ergebnisse viel leichter und es wird schwieriger, einen Unterschied zwischen den Gruppen zu belegen. In der Abbildung 11-5 ist derselbe Unterschied zwischen den Medianwerten dargestellt, weil der Abstand der beiden Dreiecke zueinander gleich groß ist. Die Basis ist aber deutlich breiter, so dass sich die Dreiecke unterschiedlich stark überlappen. Je größer die Streuungsbreite, je höher die Standardabweichung, umso weniger können wir behaupten, dass es sich um zwei unterschiedliche Populationen handelt. Bei einer hohen Variabilität scheint es fast unmöglich, dass wir jemals einen signifikanten Unterschied zwischen den Gruppen belegen können. Doch keine Angst, auch bei stark streuenden Werten können signifikante Unterschiede auftreten.

Abb. 11-5 Unterschiedlich überlappende Streubreiten
Nach allem, was wir bisher wissen, scheint das fast unmöglich. Aber es gibt zwei Wege. Der erste besteht darin, dass wir nur nach sehr großen Unterschieden suchen. Die Dreiecke rücken dann deutlich weiter auseinander und überlappen sich weniger. Bei einer großen Streuung der Daten werden auch große Unterschiede signifikant. Wenn wir aber nach kleinen Unterschieden suchen, dann bleibt uns noch der zweite, viel wichtigere Weg. Wir können nämlich einen Schlankmacher einsetzen. Wir können die Basis jedes Dreiecks verschmälern, indem wir die Stichprobe vergrößern. Wenn wir die Fallzahl erhöhen, dann streben die stark streuenden Werte ihrem Mittelwert zu. Die Box-Plots werden schmaler, die Standardabweichungen werden kleiner und die Teststatistik bzw. Prüfgröße verschiebt sich zu Gunsten der Alternativhypothese. Die Abbildung 11-6 zeigt dieselben Gruppen. Auf der rechten Seite wurde die Stichprobe drastisch erhöht. Wahrscheinlich werden viele ungläubig Staunen, wie es gelingen kann, aus einem nicht-signifikanten Unterschied, einer großen Überlappung, einen klaren signifikanten Unterschied zu kreieren. Aber genau das ist das Prinzip. Bei einer kleinen Stichprobe begünstigen wir die Nullhypothese und damit einen hohen ß-Fehler. Wir können nicht erwarten, dass wir bei kleinen Stichproben einen signifikanten Unterschied finden. Es sei denn, der Unterschied ist relativ groß. Eine Bemerkung für die Erfahrenen in der Statistik: Die gewählten Abbildungen erfüllen einen pädagogischen Zweck. Sie sollen hier nur ausdrücken, welche überragende Bedeutung der Stichprobengröße in der Berechnung der Prüfgröße zukommt.
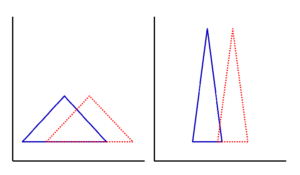
Abb. 11-6 Verminderte Streubreite bei größerer Fallzahl
Wir sollten die Hoffnung nicht aufgeben, signifikante Ergebnisse zu produzieren, denn wir können theoretisch jeden Unterschied als statistisch signifikant ausweisen, wenn wir die Stichprobe nur ausreichend groß wählen. Selbst kleinste Unterschiede erhalten so eine scheinbare Bedeutung. Bei großen Datensammlungen von Tausenden Patienten, wie sie in Registern üblich ist, besteht die Gefahr, dass selbst kleine und völlig unwichtige, klinisch überhaupt nicht relevante Unterschiede signifikant werden. Die Signifikanz verliert hier vollständig ihre Bedeutung, denn durch die hohe Fallzahl geben wir der Nullhypothese überhaupt keine Chance. Deshalb sollten wir neben der Signifikanz auch immer darauf blicken, wie groß der absolute Unterschied zwischen den Gruppen tatsächlich ist.
Ein interessantes Beispiel ist der Versuch der Firma Novartis, einen AT1-Antagonisten zur Vorbeugung des Diabetes mellitus zu verwenden. Nach einer fünfjährigen Behandlung mit Valsartan und einer Verhaltensumstellung gelang es, das neue Auftreten von Diabetes mellitus von 36,8 Prozent auf 33,1 Prozent signifikant zu senken (0,01). In dieser prospektiv-randomisierten Doppelblindstudie (n=9306) traten alle anderen kardiovaskulären Komplikationen gleich häufig auf. Dieser geringe Unterschied von 3,7 Prozent wurde nur signifikant aufgrund der hohen Fallzahl. Die klinische Relevanz bleibt fraglich – nach fünfjähriger Dauerbehandlung. Außerdem wurde in derselben Studie die Substanz Nateglinide getestet, die ebenfalls von der Firma Novartis hergestellt wird und vermehrt Insulin freisetzen soll. Nateglinide zeigte in allen Zielkriterien keinen Unterschied zu Placebo. Immerhin wurden 43.000 Patienten daraufhin überprüft, ob sie für die Studie geeignet waren.
Betrachten wir ein einfaches Beispiel, um das bisher Gelernte auch anzuwenden. Stellen wir uns vor, dass auf einem wissenschaftlichen Kongress ein randomisierter Vergleich zwischen zwei Operationsverfahren vorgestellt wird, die Entfernung des Kopfes der Bauchspeicheldrüse nach Kausch/Whipple (PD) und dem Erhalt des Magenausgangs (PPPD). In der Studie wird eine Sterblichkeit von 2,3 Prozent vs 5,6 Prozent und Komplikationsrate von 35 Prozent vs 46 Prozent beschrieben. Die Lebensqualität, der Schmerzscore und die Magenmotilität sind nach PD geringer. Um zu überprüfen, ob die beschriebenen Unterschiede wirkliche Unterschiede sind, wurden mehrere Signifikanztests durchgeführt. Alle oben beschriebenen Unterschiede waren nicht signifikant. Die Untersucher folgern aus ihren Ergebnissen, dass kein Unterschied zwischen PD und PPPD existiert. Dennoch empfehlen sie die PPPD. Ist das logisch? Ist das richtig? Wir können anhand der Daten keines der beiden Verfahren bevorzugen, weil wir einen signifikanten Unterschied nicht haben nachweisen können. Wir haben uns aufgrund der nicht-signifikanten Ergebnisse für die Nullhypothese entschieden. Eine ernsthafte Empfehlung entbehrt hier jeder Grundlage. Bedenklich ist zusätzlich, dass die angeführten nicht-signifikanten Unterschiede klinisch sehr relevant sind. In der PD-Gruppe ist die Sterblichkeit nur halb so hoch wie in der PPPD-Gruppe, und auch die Komplikationsrate ist mit 11 Prozent deutlich niedriger. Warum wurde dieser deutliche Unterschied nicht signifikant? Weil die Patientenzahl in der Studie zu klein war. Es darf hier ein typischer ß-Fehler unterstellt werden. Bei höherer Fallzahl wären die dieselben Unterschiede signifikant geworden und dann hätten die Untersucher die PD empfehlen müssen, also genau das Gegenteil von dem, was die Untersucher mitgeteilt haben.
Nachdem wir nun wissen, wie die Signifikanzen und Stichprobengrößen zusammenhängen, sollten wir den Schlussfolgerungen von Forschern immer mit Skepsis begegnen und ihnen nicht blind vertrauen. Wenn die Studie sorgfältig und ausreichend beschrieben wurde, dann können wir uns leicht einen eigenen Eindruck verschaffen. Manchmal stehen die Folgerungen der Autoren auf ganz wackeligen Füßen und manchmal sind sie einfach falsch.
Bisher haben wir immer Studien unterstellt, die einen Unterschied zwischen den Therapieverfahren nachweisen wollten. Es gibt aber auch Situationen, in denen wir die Gleichwertigkeit beweisen wollen. Mit unserem bisherigen Ansatz gelingt das nicht. Die Nullhypothese sagt nur, dass es keinen relevanten Unterschied gibt. Sie sagt nicht, dass beide Verfahren gleichwertig sind. Studien über die Gleichwertigkeit verschiedener Verfahren sind aber genauso möglich wie Studien über die Verschiedenartigkeit. Sie sind nur von der Studiengestaltung und den Berechnungen etwas aufwendiger.
Warum ist das Signifikanzniveau von 0,05 nur als willkürlich festgelegt und nicht als dogmatisch gesichert anzusehen? Weil es Gründe geben kann, davon abzuweichen. Nehmen wir an, jemand entdeckt ein neues nebenwirkungsarmes Schmerzmittel, das deutlich preiswerter als ein Konkurrenzprodukt ist und noch effektiver in der Schmerzausschaltung sein soll. In einer vergleichenden Studie wurden die Schmerzen gemessen und nachgewiesen, dass weniger Schmerzmittel gegeben werden müssen (p=0,12), um die Schmerzen gleichermaßen zu bekämpfen. Wenn wir bei dem Signifikanzniveau von 0,05 bleiben, dürfen wir die Nullhypothese nicht ablehnen, weil der Unterschied nicht signifikant ist. Wir könnten in dieser Situation aber auch sagen, dass wir auf Grund der vermuteten höheren Potenz und wegen der geringeren Nebenwirkungen, das Signifikanzniveau auf 0,15 erhöhen und damit bewusst einen höheren α-Fehler begehen. Allerdings müssen wir die Festlegung des Signifikanzniveaus fairerweise vor Beginn der Studie festlegen und nicht erst, wenn die Ergebnisse vorliegen.