Hypothesen und Irrtümer
10. Hypothesen und Irrtümer
Was ist eine Hypothese? „Hypothese“ ist zunächst ein Ausdruck, den wir im Alltag eher selten verwenden. Er lässt sich aus der altgriechischen Sprache ableiten und meint eine Vermutung oder Unterstellung, die wir zwar als gültig annehmen, aber die wir noch nicht als hinreichend bestätigt ansehen. Wir verstehen darunter Vermutungen, die wir über Sachverhalte anstehen. Darunter fallen nicht nur wissenschaftliche Fragestellungen, sondern auch alltägliche. Menschen sind „Hypothesentester“. Wir stellen über Alles und Jeden Vermutungen an und überprüfen dann, ob sie zutreffen.
Im wissenschaftlichen Kontext gibt es zwei Arten von Hypothesen, die wir statistische und deterministische Hypothesen nennen werden. Obgleich wir es im Folgenden hauptsächlich mit statistischen Hypothesen zu tun haben, sollten wir den Unterschied zwischen beiden Arten kennen, weil dadurch die weiteren Ausführungen verständlicher werden. Wir werden mit den einfachen und weniger komplizierten deterministischen Hypothesen beginnen. Wir stellen drei deterministische Hypothese auf: „ein Ball ist rot“, „alle Reiher haben einen spitzen Schnabel“ und „einige Katzen haben keinen Schwanz“. Die Beispiele klingen irgendwie gekünstelt und sehr schlicht, aber sie wurden absichtlich so einfach gewählt, um etwas zu verdeutlichen. Alle drei Hypothesen oder Behauptungen wollen wir jetzt daraufhin überprüfen, ob sie wahr oder falsch sind. Den ersten Satz „ein Ball ist rot“ können wir leicht dadurch bestätigen, indem wir einen einzigen roten Ball finden. Es können natürlich auch mehrere rote Bälle sein, aber ein einziger würde genügen, damit wir den Satz definitiv und für immer für wahr halten. Klingt doch einfach, oder? Versuchen wir nun, diesen Satz zu widerlegen. Was müssten wir tun, um die Behauptung als falsch zu beweisen. Wir müssten alle Bälle in unserer Welt, also alle Bälle, die es gibt, die es gab und die es geben wird, auf ihre Farbe untersuchen. Das ist schlichtweg nicht möglich. Sätze über einzelne Gegenstände können zwar bestätigt werden, – durch ein einziges Beispiel -, aber sie können niemals widerlegt werden. Selbst eine Trillion nicht-roter Bälle widerlegt nicht definitiv, dass nicht irgendwo ein einziger kleiner roter Ball existiert. Es ist zwar extrem unwahrscheinlich, aber nicht ausgeschlossen. Vielleicht hat irgendjemand einen roten Ball als extrem seltenen Schatz in einem Tresor verschlossen. Sätze über einzelne Gegenstände können wir demnach eindeutig bejahen, aber nicht definitiv verneinen. Wer also nach absoluter Sicherheit strebt, wird verzweifeln, wenn er einen solch einfachen Satz widerlegen möchte.
Denken wir jetzt über den Satz mit den Reihern nach. Können wir tatsächlich alle Reiher, die es gibt, daraufhin untersuchen, ob sie einen spitzen Schnabel haben? Nein, auch das können wir nicht. Wir können solche Sätze, die den Ausdruck „alle“ enthalten, niemals sicher bestätigen. Wir können uns nicht sicher sein, dass sie wahr sind. Aber wir können uns ganz schnell davon überzeugen, dass der Satz falsch ist. Ein einzelner Reiher mit einem krummen Schnabel würde nämlich bedeuten, dass der Satz falsch ist. Vorausgesetzt, dass niemand uns einen anderen Vogel mit einem krummen Schnabel als Reiher untergeschoben hat und uns damit zu täuschen versucht, kann ein einzelnes Faktum „Alle-Sätze“ widerlegen. Jetzt überprüfen wir den Satz über die Katzen. Können wir den Satz bestätigen? Ja, wenn wir mehr als eine Katze ohne Schwanz sehen, dann ist der Satz „einige Katzen haben keinen Schwanz“ definitiv wahr. Können wir ihn auch widerlegen? Nein, das können wir nicht. Auch hier müssten wir alle Katzen untersuchen, um den Satz definitiv zu widerlegen. Die Aussage über Katzen verhält sich demnach wie die erste Aussage über rote Bälle.

Tab. 10.1 Möglichkeit der Bestätigung oder Widerlegung
Fassen wir zusammen, was wir bis jetzt wissen: Es besteht eine bemerkenswerte Asymmetrie. Einige Sätze können wir sicher bestätigen und andere nicht. Einige Sätze können wir sicher widerlegen und einige können wir niemals widerlegen. Entweder können wir das Eine oder das Andere, aber niemals Beides. Interessanterweise sind wir gerade als Wissenschaftler bestrebt, allgemeinverbindliche Gesetzmäßigkeiten zu finden und zu formulieren, die durch solche Alle-Sätze ausgedrückt werden. Als Wissenschaftler sind wir nicht an Anekdoten oder Einzelereignissen interessiert. Wir wollen vielmehr herausfinden, wie sich Sachverhalte regelhaft verhalten, um Prognosen aufzustellen und technologische Anwendungen zu entwickeln. Wir können nur dann verlässliche Aussagen über zukünftige Ereignisse aufstellen, wenn sich die Ereignisse immer und immer wieder so verhalten, wie wir vermuten. Wenn wir ein Naturgesetz formulieren, dann unterstellen wir, dass sich die Natur immer so verhält. Darauf beruhen einerseits unsere Prognosen und andererseits unsere Technologie. Kupfer leitet unter normalen Bedingungen Strom und Stahl ist relativ stabil. Eine Kugel läuft nach bestimmten Gesetzen eine schiefe Ebene herab und auch eine chemische Reaktion folgt reproduzierbaren Gesetzen. Alle diese Gesetzmäßigkeiten werden in Sätzen beschrieben, die den Alle-Sätzen entsprechen. Leider haben wir aber gerade erkennen müssen, dass Hypothesen und Theorien über Gesetzmäßigkeiten niemals absolut zu bestätigen sind. Das Einzige, was wir erreichen können, sind definitive Widerlegungen. Aus diesen Gründen wird gefordert, dass sich gute Wissenschaft dadurch auszeichnet, ihre Hypothesen und Theorien dem Versuch auszusetzen, sie zu widerlegen. Ein guter Wissenschaftler sollte versuchen, seine Theorie zu widerlegen. Er sollte nicht versuchen, sie zu bestätigen, denn eine definitive Bestätigung wird nicht gelingen. Erst dadurch, dass es nicht gelingt, die Theorie zu widerlegen, wird die Theorie indirekt bestätigt.
Möglicherweise fragen sich einige: Warum müssen wir denn alles ganz sicher wissen? Reicht es nicht aus, 1.000 Katzen zu untersuchen, und wenn alle keinen Schwanz haben, die Behauptung als „vorläufig wahr“ zu akzeptieren? Ja, das ist unser alltägliches und bewährtes Vorgehen. Wir geben uns in der Regel damit zufrieden. Aber definitiv sicher können wir uns nicht sein.
Wenden wir uns jetzt den statistischen Hypothesen zu. Sie haben nicht die Form: „Katzen sind schwarz“, sondern „Katzen sind zu 32 Prozent schwarz“. Statt „ein Ball ist rot“ lauten sie zum Beispiel: „12 Prozent aller Bälle sind rot“. Wie können wir solche Hypothesen bestätigen oder widerlegen. Indem wir in guten Studien valide Ergebnisse generieren, einen Signifikanztest durchführen und dann entscheiden, ob wir die Hypothese für richtig oder falsch halten. Wir könnten auf den ersten Blick meinen, es verhält sich so, wie bei den obigen deterministischen Hypothesen. Das trifft aber nicht zu. Es besteht ein entscheidender Unterschied zwischen beiden Hypothesenarten. Wenn sich eine deterministische Hypothese einmal für definitiv wahr oder falsch erwiesen hat, dann bleibt sie das für immer – vorausgesetzt, wir vertrauen auch weiterhin den Daten, die zur Widerlegung oder Bestätigung führten. Bei statistischen Hypothesen verhält es sich grundsätzlich anders. Sie sind immer nur vorläufig wahr oder falsch. Wir können uns niemals sicher sein, dass sie zutreffen oder nicht. Es kann immer sein, dass wir eine statistische Hypothese für wahr halten und unser Urteil dann im Lichte neuer Daten revidieren. Es könnte sein, dass eine Studie eine Hypothese unterstützt und zwei darauf folgende Studien eher die Hypothese in Frage stellen. Statistische Hypothesen sind immer nur vorläufig bestätigt oder widerlegt und niemals endgültig. Dieser entscheidende Unterschied ist der Grund, warum eine Hypothesentestung auf den ersten Blick so verwirrend sein mag. Wenn wir aber einmal verstanden haben, dass statistische Hypothesen IMMER nur vorläufig gelten, dann sollten wir eigentlich das Hauptproblem begriffen haben.
Im vorigen Kapitel hatten wir immer nur eine Hypothese aufgestellt und wir hatten uns gefragt, ob wir sie für richtig halten. Wir waren aber in unserer Sprache etwas „schlampig“. Wir haben uns nicht darüber geäußert, was wir tun, wenn wir die Hypothese ablehnen. De facto behaupten wir damit doch das Gegenteil der Hypothese. Wenn wir zwei Verfahren miteinander vergleichen, dann stellen wir genau genommen mehr als eine Hypothese auf. Wir formulieren in der Regel zwei Hypothesen, die sich gegenseitig ergänzen: eine sogenannte Nullhypothese (H0) und eine alternative Hypothese (HA). Den Begriff „Nullhypothese“ haben wir sicherlich schon früher gehört. Wir können ihn uns einfach merken, indem wir sagen, dass der Unterschied zwischen den Gruppen null und nichtig ist. Die Nullhypothese lautet, dass es KEINEN Unterschied zwischen den beiden Gruppen A und B gibt: „H0: A=B“. Die Alternativhypothese lautet dagegen, dass es einen Unterschied gibt: „HA: A≠B“. Es gibt natürlich noch andere Varianten, wie solche Hypothesen (H0 oder HA) formuliert werden können, aber das würde uns hier nur verwirren.
Warum nennen wir sie eigentlich Alternativ- bzw. Nullhypothese? Wir sind als Forscher daran interessiert, etwas Neuartiges, etwas Besseres zu entwickeln. Dieses Bessere nennen wir das neue alternative Verfahren. Deshalb beschreiben wir den zu erwartenden Unterschied in der Alternativhypothese. Intuitiv wünschen wir, die Alternativhypothese zu begünstigen. In der Nullhypothese wird dagegen behauptet, dass es keinen Unterschied zwischen den Verfahren gibt. Wir behaupten in der Nullhypothese, dass unser neues Verfahren nicht besser ist. Da wir aber von unserem neuen Verfahren überzeugt sind, wollen wir diese Nullhypothese widerlegen. Wir wollen beweisen, dass die Nullhypothese nicht zutrifft, sondern die Alternativhypothese. Deshalb streben wir nach kleinen p-Werten. Wenn es nämlich unwahrscheinlich ist, dass die Nullhypothese zutrifft, dann ist das ein indirekter Beleg dafür, dass das neue Verfahren besser ist. Gute Wissenschaftler, die neue bessere Methoden entwickeln, generieren niedrige signifikante p-Werte.
Warum ist es wichtig, dass wir zwei Hypothesen überprüfen und nicht nur eine? Weil wir uns am Ende der Studie für eine der beiden entscheiden müssen. Wenn wir nur eine einzige Hypothese aufstellen und wir sie nicht für richtig halten, dann hängen wir in der Luft, weil keine Alternative formuliert wurde. Das Ergebnis des Signifikanztestes legt fest, ob wir der Nullhypothese zustimmen oder nicht. Wenn wir der Nullhypothese nicht zustimmen wollen, weil der p-Wert zu klein ist, was machen wir dann? Sich jetzt unschlüssig zu enthalten, ist eine schlechte Option. Das würde nämlich bedeuten, dass unsere Studie weitgehend wertlos ist und wir möglicherweise viele Ressourcen und Zeit verschwendet haben. Eine Entscheidung muss her, so oder so.
Einfache Beispiele sollen die Situation erhellen. Nehmen wir an, wir behandeln einen Patienten mit Bauchspeicheldrüsenkrebs und Lebermetastasen mit dem Medikament „Krebstod“. Damit erreichen wir nach der Diagnosestellung ein medianes Überleben von 14 Monaten. Ein neues Medikament „Eraser“ wird uns jetzt angeboten, weil es das Überleben verlängern soll. Es ist doppelt so teuer wie „Krebstod“. In einer vergleichenden Studie wird es gegen „Krebstod“ untersucht. Das mediane Überleben beträgt in der Gruppe „Krebstod“ 15 Monate und in der Gruppe „Eraser“ 23 Monate. Wir fragen uns jetzt, ob der Unterschied von acht Monaten zufällig entstand oder Folge des neuen Medikamentes ist. Wir führen einen Signifikanztest durch, der den p-Wert von 0,03 ergibt, d.h. dass die Studienergebnisse unter der Annahme der Nullhypothese mit einer Wahrscheinlichkeit von drei Prozent auftreten. Das ist so gering, dass wir die Nullhypothese verwerfen und uns für die Alternativhypothese entscheiden, die besagt, dass „Eraser“ besser ist als „Krebstod“.
Konstruieren wir ein anderes Beispiel. Wir messen die Cholesterinwerte von 200 Patienten, die wir als Hausarzt schon seit Jahren mit dem bewährten Medikament „Cholsenker“ behandeln. Die Werte betragen 180±10 mg/dl. Ein Pharmavertreter zeigt uns randomisierte Studien, in denen ein neues Medikament „Cholex“ die Werte um weitere 20 mg/dl senkte. Wir vertrauen den Studien und setzen das etwas teurere Medikament bei allen 200 Patienten ein. Da wir wissen wollen, ob die Mehrkosten gerechtfertigt sind, entschließen wir uns, nach sechs Monaten die Cholesterinwerte zu kontrollieren und mit den vorhergehenden Werten zu vergleichen. Wir würden jetzt erwarten, dass die Cholesterinwerte ungefähr 160±10 mg/dl betragen, wenn „Cholex“ hält, was es verspricht. Die Werte betragen bei den 200 Patienten zu unserer Überraschung aber 170±10 mg/dl. Sie sind nicht so weit gesunken, wie wir erwartet haben. Was schließen wir daraus? Wirkt „Cholex“ nicht, wie versprochen? Natürlich konnten wir nicht ernsthaft erwarten, dass wir tatsächlich exakt 160 mg/dl messen. Aber wir hätten uns sehr gefreut, wenn es sogar weniger als 160 mg/dl gewesen wäre, denn schließlich setzen wir das teurere Medikament ein, um das Cholesterin um über 20 mg/dl zu senken. Hätten wir 150 mg/dl gemessen, hätten wir nicht gezögert, das Medikament weiterzuempfehlen. Wenn wir dagegen 180 mg/dl gemessen hätten, dann wären wir äußerst enttäuscht gewesen und würden vermuten, dass das eine Medikament so gut ist wie das andere. Wir müssen uns also fragen, ab welchem Wert wir bereit wären, dem neuen Medikament eine nachweislich bessere Wirkung zuzuschreiben. Wirkt das Medikament überhaupt?

Wir sind verunsichert, vertrauen aber den Werbebroschüren des Pharmaunternehmens und behandeln die Patienten weiter mit dem neuen teuren „Cholex“. Nach weiteren sechs Monaten kontrollieren wir wieder alle Werte und messen dieses Mal 165±10mg/dl. Das sieht doch schon besser aus. „Cholex“ scheint tatsächlich zu wirken. Wir sind froh und der Pharmavertreter, der zwischenzeitlich um seinen Umsatz bangte, hat auch mit seinem nervösen Zucken aufgehört. Wir bleiben bei unserem Vorgehen und sind überzeugt, dass wir den Patienten geholfen haben. Doch haben wir das wirklich? Haben wir die vermehrten Ressourcen tatsächlich zum Wohle der Patienten eingesetzt? Diese Frage können wir weder bejahen noch verneinen. Wir können sie einfach nicht beantworten. Denn wir haben nur auf die Cholesterinwerte geschaut und die haben wir etwas gesenkt. Ob wir dadurch eine Krankheit abgeschwächt, positiv beeinflusst oder sogar Komplikationen verhindert haben, wissen wir nicht. Wir haben einfach unterstellt – auch eine unbestätigte und sehr umstrittene Hypothese -, dass die kardiovaskulären Komplikationen weiter gesenkt werden, wenn wir das Cholesterin weiter senken.
Neugierig kontrollieren wir nach 12 Monaten erneut die Cholesterinwerte, die jetzt überraschenderweise 175±10mg/dl betragen. Wie sollen wir diese Werte jetzt bewerten? Haben wir uns von Anfang an geirrt? Wirkt das neue Medikament doch nicht besser? Sollen wir wieder das alte und preiswerte Medikament verschreiben? Wie können wir diese sich aufdrängenden Fragen beantworten und die bestehende Ungewissheit beseitigen? Nur dadurch, indem wir geeignete statistische Tests verwenden. Indem wir berechnen, wie wahrscheinlich die Daten unter der Hypothese auftreten, haben wir ein Maß, die p-Werte, mit denen wir sinnvolle und nachvollziehbare Entscheidungen treffen können. Wir sollten uns in solchen Situationen weniger von unserer Intuition als von adäquaten Signifikanztests leiten lassen, denn es gibt keine bessere Methode, die von anderen nachvollziehbar ist. Keiner kann uns zwingen, Signifikanztests durchzuführen. Aber wenn wir es nicht tun, dann haben wir die Schwierigkeit, unsere Entscheidung für oder gegen das Medikament zu begründen. Wir können intuitiv handeln und aus unserer Erfahrung schöpfen, aber die lässt uns bekannter Weise sehr häufig im Stich oder führt uns im schlimmsten Fall in die Irre. Die Signifikanztests sind methodisch das Beste, was wir haben. Allerdings verhindern die Tests nicht, dass wir uns nicht auch irren können. Deshalb wenden wir uns jetzt den Irrtumsmöglichkeiten zu.
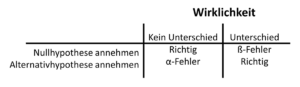
Tab. 10.2 Irrtumsmöglichkeiten bei der Hypothesentestung
Wenn wir uns für oder gegen die Nullhypothese entscheiden, dann können wir uns irren und eine Fehlentscheidung treffen. Irrtümer sind immer möglich. Stellen wir unsere beiden Entscheidungsmöglichkeiten den beiden realen Zuständen in einer Tabelle gegenüber. Wir erhalten eine Vierfeldertabelle, wie wir sie bereits aus den Abschnitten zur Diagnostik kennengelernt haben. Die Wirklichkeit wird in den Spalten angegeben. Entweder es besteht tatsächlich kein Unterschied zwischen den untersuchten Verfahren oder aber es besteht ein Unterschied. De facto kennen wir die Wirklichkeit nicht, denn sonst hätten wir die Studie nicht durchgeführt. Wir kennen nur das Ergebnis unseres Testes. Deshalb können wir uns nur an den Zeilen ausrichten. In der oberen haben wir uns zugunsten der Nullhypothese entschieden und in der unteren zugunsten der Alternativhypothese. Wenn wir uns für die Nullhypothese entscheiden und damit festlegen, dass es keinen Unterschied zwischen den beiden Gruppen gibt, dann können wir uns irren. Nämlich genau dann, wenn tatsächlich ein Unterschied besteht und wir dennoch in den Studien den Unterschied nicht nachweisen konnten.
Wir wollen diese Irrtumsmöglichkeit umschreiben. Immer dann, wenn wir in Studien keinen Unterschied zwischen zwei Gruppen feststellen und dennoch einer vorliegt, dann begehen wir diesen Fehler. Stellen wir uns vor, wir stehen als Jäger stundenlang auf einem Hochsitz und erspähen kein Wild. Wir schließen aus der Situation, dass es im Jagdgebiet nichts zu jagen gibt. Wie dumm nur, dass sich die Hasen alle ein Stelldichein unter dem Hochsitz gegeben haben, weil sie dort von uns nicht gesehen werden können. Wir begehen in diesen Fällen einen Irrtum, der ß-Fehler genannt wird. Diesen Fehler werden wir in einem anderen Abschnitt über die Fallzahlberechnung diskutieren.
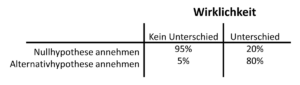
Tab. 10.3 Wahrscheinlichkeiten bei der Hypothesentestung
Wenn wir uns für die Alternativhypothese entscheiden, weil es einen signifikanten Unterschied gibt, dann können wir uns ebenfalls irren. Die Alternativhypothese besagt, dass es einen Unterschied gibt. Und wenn wir das behaupten, dann können wir einem α-Fehler aufgesessen sein. Wir haben einen Unterschied gesehen, obwohl er real nicht existiert. Wir behaupten dass das Medikament besser ist als ein anderes, aber in Wirklichkeit sind sie beide gleich gut. Wir behaupten, dass eine Operationsmethode zu weniger Komplikationen führt, aber in Wirklichkeit sind die Komplikationsraten vergleichbar. Das einzige, was hier tröstlich wirkt, ist die Tatsache, dass wir nicht beide Fehler gleichzeitig begehen können. Ein ß-Fehler kann ja nur dann auftreten, wenn wir in der Studie keinen Unterschied finden, wir uns deshalb folgerichtig für die Nullhypothese entscheiden und dennoch real ein Unterschied besteht. Gleichzeitig zum ß–Fehler können wir den α-Fehler nicht begehen, denn dazu müssten wir uns für die Alternativhypothese entscheiden.
Können wir diese Irrtümer irgendwie begrenzen oder kontrollieren? Ja und nein. Wir haben einen direkten Einfluss auf den α-Fehler. Indem wir das Signifikanzniveau festlegen, d.h. ab welcher Wahrscheinlichkeit wir uns für die Alternativhypothese entscheiden, können wir den α-Fehler größer oder kleiner werden lassen. Allgemein wird heute eine Nullhypothese abgelehnt, wenn die bedingte Wahrscheinlichkeit unter fünf Prozent liegt. Diese 5%-Grenze ist eine willkürliche Festsetzung und es kann in manchen Situationen gute Gründe geben, diese Grenze nach oben oder unten zu verschieben. Wenn wir das Signifikanzniveau auf fünf Prozent festgelegt haben, dann entscheiden wir uns bei einem p-Wert unter 0,05 gegen die Nullhypothese und für die Alternativhypothese. Damit beschränken wir den α-Fehler bzw. die Irrtumswahrscheinlichkeit auf unter fünf Prozent.
Wenn wir den α-Fehler weiter vermindern wollen, dann müssen wir das Signifikanzniveau erniedrigen. Setzen wir α=0,01, dann beschränken wir den α-Fehler auf 1 Prozent. Wir immunisieren damit quasi die Nullhypothese, denn es wird immer schwieriger, die Nullhypothese abzulehnen. Wir lassen der Alternativhypothese weniger Chancen. Wenn wir dagegen das Signifikanzniveau auf 0,1 festlegen würden, dann wird es leichter, die Nullhypothese abzulehnen. Zugleich nimmt aber das Risiko zu, einen α-Fehler zu begehen. Deshalb hat sich im wissenschaftlichen Alltag allgemein durchgesetzt, das Signifikanzniveau auf fünf Prozent festzusetzen. Egal, wie wir das Signifikanzniveau festlegen, das Risiko eines α-Fehler bestimmt immer.
Jetzt verstehen wir auch den Unterschied zweier Redewendungen: „es besteht ein Unterschied von 20 mg/dl“ und „es besteht ein signifikanter Unterschied von 20 mg/dl“. Im ersten Ausdruck wird lediglich formuliert, wie groß der Unterschied zwischen zwei Gruppen ist. Im zweiten Ausdruck wird zugleich gesagt, dass dieser Unterschied jenseits des Signifikanzniveaus liegt und wir bereit sind, die Nullhypothese abzulehnen. Der erste Ausdruck meint: „Es gibt zwar einen messbaren Unterschied, aber den werten wir nicht so richtig. Eigentlich gehen wir davon aus, dass dieser Unterschied rein zufällig entstand und nicht wirklich zeigt, dass ein Unterschied zwischen den Gruppen existiert. Wir sollten den Unterschied eher als Modulation ansehen“ Nicht-signifikante Unterschiede sind damit „Schein-Unterschiede“, sie existieren als Unterschiede nicht wirklich. Sie sind nur Ausdruck der Variabilität der Daten und wir könnten genauso gut sagen, dass es keinen Unterschied gibt. Signifikante Unterschiede sind dagegen tatsächliche Unterschiede, denn wir sind bereit, trotz des möglichen -Fehlers, einen wirklichen Unterschied zu unterstellen. Die Konsequenz dieser Redeweise springt sofort ins Auge. Wir erwarten ab sofort bei vergleichenden wissenschaftlichen Aussagen immer die Angabe des p-Wertes, damit wir beurteilen können, ob das Ergebnis signifikant ist. Alle anderen Unterschiede werden als scheinbare Unterschiede bewertet.
Signifikante Ergebnisse sind die Beute des erfolgreichen Forschers. Nicht-signifikante Ergebnisse sind unerwünscht. Ja, sie werden geradezu verachtet. Sie scheinen das Stigma eines erfolglosen Forschers zu sein, denn es ist ihm offensichtlich nicht gelungen, eine neue Idee zu entwickeln, die tatsächlich besser ist als das Hergebrachte. Der Forscher möchte in seiner Studie beweisen, dass seine neue Methode der alten überlegen ist. Und dazu benötigt er einen signifikanten Unterschied. Die gesamte Reputation eines Forschers und Wissenschaftlers hängt davon ab, wie viel signifikante Forschungsergebnisse er publiziert hat. Die Publikationen in den zugehörigen Fachjournalen ist der Gradmesser des Erfolges. Nicht-signifikante Ergebnisse werden nachweislich seltener publiziert und viele Forscher halten sie für nicht publikationswürdig. Diese Sichtweise des Forschers ist aber einseitig verzerrt. Der Forscher offenbart natürlich nicht gern seine „Niederlage“ und verschweigt die nicht-signifikanten Ergebnisse. Aber er hat die Studien durchgeführt und für die wissenschaftliche Gemeinschaft als solche sind auch diese Ergebnisse von großem Wert. Es ist wichtig, zu wissen, ob Verfahren sich nicht unterscheiden. Das hilft einerseits bei der Bewertung der Verfahren und es schützt davor, dass andere Forscher dieselben Studien mit nicht-signifikanten Ergebnissen wiederholen. Die Ergebnisse jeder sorgfältigen Studie sind interessant und wichtig und sollten deshalb unbedingt publiziert werden.
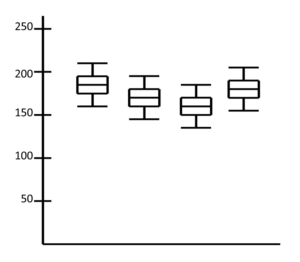
Abb. 10-4 Cholesterinwerte zu verschiedenen Zeitpunkten
Blicken wir zurück auf unsere Cholesterinmessungen. Unser damaliges Problem war, dass wir nicht wussten, wie wir die unterschiedlichen Messergebnisse interpretieren sollten, die in der Abbildung 10-4 als Box-Plots zu sehen sind. Die Werte schwankten zwar, aber sanken nicht so sehr, wie wir es erwartet hatten. Wir hatten primär keinen Signifikanztest angewendet, so dass wir die Schwankungen nicht zu einer fundierten Entscheidung nutzen konnten. Das wird uns in Zukunft nicht mehr passieren. Wir führen in Zukunft in ähnlichen Situationen einen Signifikanztest durch oder fordern einen ein. Dann betrachten wir die entsprechenden p-Werte und richten danach unsere Entscheidung.