Hypothesen und Signifikanzen
Beginnen werden wir diesen Abschnitt mit dem Problem alternativer Handlungen, denn bekanntermaßen führen viele Wege nach Rom. Es gibt für die Ziele, die wir anstreben, häufig mehrere alternative Wege, sie zu erreichen. Wenn wir einen bestimmten Zweck verfolgen, dann könnte es sein, dass wir verschiedene Mittel einsetzen können, um erfolgreich unser Ziel zu erreichen. Wenn es Alternativen gibt, müssen wir zwischen ihnen wählen. Wir können schließlich nur einen der Wege gehen. Und welchen Weg wir wählen, hängt einerseits von unseren Wünschen und Prämissen ab, aber andererseits auch von den Vor- und Nachteilen der Alternativen. Wenn wir zum Beispiel mit der Bahn von Hamburg nach Berlin fahren wollen, dann würden wir nicht über Hannover fahren, weil der Weg weiter ist. Es könnte aber sein, dass wir in Hannover einen kurzen Aufenthalt einlegen möchten, um Freunde zu besuchen, so dass wir dennoch eine Fahrkarte über Hannover lösen.
Im medizinischen Alltag ist es eher die Regel als die Ausnahme, dass wir vor Alternativen stehen. Als Ärzte wägen wir gemeinsam mit dem Patienten die Vor- und Nachteile der alternativen Verfahren ab und setzen gezielt dasjenige Verfahren ein, das in der speziellen individuellen Situation das günstigere Ergebnis erwarten lässt. Um gute Entscheidungen für oder wider eine bestimmte Therapie zu treffen, benötigen wir ausreichende und verlässliche Informationen über die Vor- und Nachteile der verschiedenen Verfahren. Es ist nicht ausreichend, dass der Arzt kraft seines Wissens, seiner Erfahrung und seiner Autorität festlegt, welches Verfahren für den Patienten geeignet ist. Heute entnehmen wir viele entscheidungsrelevante Informationen aus vergleichenden Studien, in denen beide Verfahren fair und gewissenhaft miteinander verglichen wurden. Wir fragen immer nach guten Gründen, warum ein Verfahren besser sein soll als ein anderes. Wenn Therapien heutzutage miteinander verglichen werden, dann fordern wir prospektiv randomisierte Studie als sogenannten Goldstandard. Was diese Studien auszeichnet, werden wir mit der „induktiven Statistik“ verstehen. Die Ergebnisse anderer Studientypen sind weniger verlässlich und führen häufiger zu Fehlentscheidungen. Sehr fundierte Argumente liegen vor, wenn die Vorteile sogar in mehreren randomisierten Studien nachweisbar sind. Dann halten wir die Vorteile für gut gesichert.
Wenden wir uns nun der Grundstruktur wissenschaftlicher Studien zu. Für jede vergleichende Studie ist es unabdingbar, dass eine Hypothese über die verschiedenen Verfahren formuliert wird. Eine sehr einfache Hypothese könnte zum Beispiel lauten, dass die Therapie A besser ist als die Therapie B. Wir könnten aber auch vermuten, dass die Therapie A schlechter ist als B oder gleichwertig. Egal, welchen Vergleich wir vornehmen wollen oder wie wir ihn sprachlich fassen werden, wir müssen eine geeignete, klar formulierte und verbindliche Hypothese aufstellen, die wir dann in der Studie überprüfen werden.
Letztlich geht es in einer Studie nur darum, diese eine einzige Hypothese zu überprüfen. Das gesamte Studiendesign und ausgewählte Model wurde dazu ausgesucht. Es mag durchaus sein, dass wir auch noch andere Fragen beantwortet wissen wollen. Aber dazu sind eigentlich neue Studien erforderlich.
Wenn wir eine Hypothese formulieren, dann verwenden wir die vergleichenden Ausdrücke „ist besser als“, „ist schlechter als“ oder „ist gleichwertig mit“. Was meinen wir damit? Die oben genannten einfachen Hypothesen waren nur Abkürzungen für längere Versionen. Statt „A ist besser als B“ hätte es lauten müssen: „die Therapie A führt zu weniger infektiösen Komplikationen als die Therapie B“ oder „die Operationsmethode A führt zu genauso vielen Rezidiven wie die Operationsmethode B“. Wenn wir etwas vergleichen, dann müssen wir zunächst angeben, was wir vergleichen, nämlich die verschiedenen Therapien A und B, und wir müssen zusätzlich definieren, wie wir sie miteinander vergleichen. Es muss deshalb in der Hypothese immer ein klares Kriterium genannt werden, ein so genanntes Zielkriterium, anhand dessen wir entscheiden, ob eine Therapie besser oder schlechter ist. Dieses primäre Zielkriterium muss in der Hypothese immer explizit genannt werden. Die gesamte Studie wird am Ende nur durchgeführt, um anhand dieses Zielkriteriums die Hypothese zu überprüfen. Es ist nicht ausreichend, nur eine Liste von mehreren Zielkriterien zu nennen, von denen wir uns nach der Durchführung der Studie dann diejenige aussuchen, die ein signifikantes Ergebnis zeigt. Solch ein Vorgehen gestattet jede Art der Manipulation und wird heute strikt abgelehnt. Wir werden in späteren Abschnitten eingehend besprechen, welche schwierigen Probleme auftreten können, wenn mehrfache Signifikanztests durchgeführt werden.
Meistens enthalten Studien außer dem primären Kriterium auch noch weitere, sogenannte sekundäre Zielkriterien. Wenn zum Beispiel in einer Krebsstudie zwei Therapien verglichen werden, dann ist in der Regel das gesamte Überleben das entscheidende primäre Zielkriterium. Schließlich geht es doch bei einer Krebsbehandlung darum, länger zu überleben. Aber in solchen Studien wird auch nach dem rückfallfreien Überleben, nach der Rückbildungsrate oder der Lebensqualität geschaut. Natürlich werden bei der Auswertung alle Zielkriterien ausgewertet und verglichen, aber streng genommen entscheidet nur das gesamte Überleben über die Hypothese. Wenn zum Beispiel zwei Operationsverfahren daraufhin überprüft werden, welches von beiden Verfahren postoperativ zu weniger Schmerzen führt, dann werden sich die Untersucher in der Studie nicht darauf beschränken, die Schmerzen als primäres Zielkriterium zu untersuchen. Sicherlich werden sie auch die Komplikationen, Rückfälle o.ä. als sekundäre Zielkriterien erfassen. Wie aber sollen wir eine Studie interpretieren, wenn im primären Zielkriterium kein Unterschied besteht und in einigen sekundären Zielkriterien die Methode B besser ist. Das klingt ein wenig nach schlechten Erfahrungen in der Schule: „Interessant geschrieben, aber Thema verfehlt und deshalb nur mangelhaft.“
An einem einfachen Beispiel wollen wir jetzt erläutern, was es bei vergleichenden Studien zu bedenken gibt, ohne dass wir uns mit den Formalien eines Studienplans aufhalten. Stellen wir uns einen Landwirt vor, der vor 50 Jahren erwog, einen speziellen Dünger auf seinen Feldern zu verstreuen, um die Ernte zu erhöhen. Da der Dünger viel Geld kostet, würde er ihn nur kaufen, wenn er tatsächlich seine Ernte und damit seine Einnahmen deutlich erhöht und damit die Kosten für den Dünger wieder ausgleicht. Um nun zu überprüfen, ob das auch zutrifft, führte er eine vergleichende Studie durch. Als Hypothese formulierte der Landwirt: der Dünger erhöht die Weizenernte nicht. Es mag hier verblüffend klingen, dass die Untersucher regelhaft pessimistisch klingen und als Hypothese formulieren, dass es keinen Unterschied zwischen den beiden Gruppen gibt. Später wird deutlich werden, dass der Grund für diese Formulierung nicht in einer allgemeinen Depression der Untersucher liegt, sondern tatsächlich sinnvoll ist.
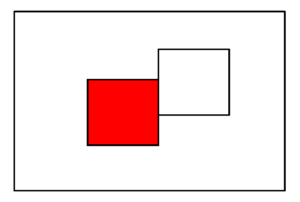
Abb. 9-1 Einfache Parzellierung
Nach einem Jahr erntete der Landwirt auf den unbehandelten, aber vergleichbaren Feldern 7,5 t/ha Weizen und auf den mit Dünger gedüngten Feldern 8,2 t/ha Weizen. Die erste Frage, die sich dem Landwirt aufdrängte, lautet: Ist der gefundene Unterschied von 0,7 t/ha zufällig entstanden oder ist er durch den Dünger bedingt. Es ist theoretisch denkbar, dass der Dünger überhaupt keinen Effekt hatte und dennoch auf den gedüngten Feldern rein zufällig in diesem Jahr mehr Weizen geerntet wurde. Das könnte sich im nächsten Jahr auch ändern. Da die Steigerung der Ernte um 0,7 t/ha den Landwirt nicht überzeugte, diskutierte er das Ergebnis mit seinen Kollegen, die bereits seit Jahren denselben Dünger verwendeten und vom positiven Effekt überzeugt sind. Diese wollten zunächst wissen, wo er gedüngt hatte. Nachdem der Landwirt die Felder beschrieben hatte, waren auch seine Kollegen verunsichert, weil er den Dünger in Bereichen ausgebracht hatte, wo bereits früher mehr geerntet wurde. Da die Ernte von vielen Faktoren wie Mikroklima, Bodenverhältnissen oder ungleich verteiltem Ungeziefer beeinflusst wird, müssen diese Faktoren in beiden Gruppen gleich verteilt sein, um einen fairen Vergleich zu ermöglichen. Das hatte der Landwirt übersehen. Deshalb entschloss er sich, einen neuen Versuch zu planen. Er teilte zunächst seine Ackerfläche in 100 gleich große Flächen ein. Für jede einzelne Fläche wählte er mit einem Münzwurf zufällig aus, ob sie gedüngt werden sollte oder nicht. Mit dieser Randomisierung bezweckte der Landwirt, die bekannten und unbekannten Einflussgrößen gleichmäßig auf beide Gruppen zu verteilen.
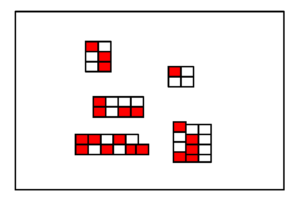
Abb. 9-2 Komplexe Parzellierung
Nach einem weiteren Jahr wertete der Landwirt seine Ergebnisse aus. Auf den 50 ungedüngten Flächen betrug die Ernte 7,1 t/ha und auf den 50 gedüngten Feldern 8,3 t/ha. Der Unterschied zwischen beiden Gruppen betrug 1,2 t/ha. Ist dieser gemessene Unterschied tatsächlich ein Beweis dafür, dass der Dünger zu einer reicheren Ernte führt oder ist auch dieses Ergebnis zufällig entstanden? Um diese Frage zu beantworten, wird ein sogenannter Signifikanztest durchgeführt. Der Test soll uns mitteilen, wie hoch die Wahrscheinlichkeit ist, dass das gefundene Ergebnis zufällig aufgetreten ist. Wie wir uns denken können und auch immer wieder lesen, gibt es viele verschiedene Tests. Wir werden hier nicht besprechen, welcher Test in welcher Situation angewendet wird, sondern uns hier auf das Prinzipielle beschränken. Allerdings soll an dieser Stelle ausdrücklich betont werden, dass der „richtige“ Test verwendet werden muss. Da solch ein Signifikanztest unter anderem das Studiendesign, die Anzahl der untersuchten Felder, die zu erwartenden zufälligen Unterschiede und den tatsächlich nachgewiesen Unterschied berücksichtigt, kann nicht ein beliebiger Test herangezogen werden, sondern nur einer, der unter den spezifischen Bedingungen geeignet ist. Vorausgesetzt, wir verwenden den richtigen Signifikanztest, dann gibt der Test eine Wahrscheinlichkeit an, einen p-Wert (probability). Dieser Wert beträgt in unserem Beispiel p=0,1. Dieser p-Wert ist in der wissenschaftlichen Literatur so etwas wie der heilige Gral. Alle ambitionierten Forscher versuchen, einen niedrigen Wert bzw. ein signifikantes Ergebnis zu erreichen.
Was drückt dieser p-Wert von 0,1 aus? Was meint die Wahrscheinlichkeit von zehn Prozent? Es ist nicht die Wahrscheinlichkeit, dass die Hypothese zutrifft. Wir können nicht sagen, dass die Hypothese zu zehn Prozent stimmt, was ziemlich wenig wäre. Es trifft auch nicht zu, dass der Dünger nur mit einer Wahrscheinlichkeit von zehn Prozent wirkt. Es ist auch nicht die Wahrscheinlichkeit der Daten, denn Daten sind, was sie sind. Daten sind Fakten. Fakten werden als solche nicht bezweifelt. Was sagt uns der p-Wert? Was ermittelt der Signifikanztest? Er berechnet eine bedingte Wahrscheinlichkeit, was komplizierter klingt, als es ist. Der p-Wert teilt uns mit, wie wahrscheinlich die Daten/Fakten auftreten, wenn die Hypothese zutrifft. Dieser kleine, aber feine Unterschied ist die Würze in der Statistik. Diesen Unterschied müssen wir verstehen. Es wird in dem Signifikanztest unterstellt, dass die Hypothese zutrifft. Dann wird berechnet, wie wahrscheinlich es ist, dass dann diese Fakten eintreten. In unserem Fall wird unterstellt, dass der Dünger nicht wirkt. Die Hypothese, die getestet wird, lautet, dass es keinen Unterschied gibt zwischen gedüngten und ungedüngten Feldern. Der gemessene Unterschied zwischen den Feldern müsste theoretisch Null sein. Wenn wir auf das Ergebnis schauen, sehen wir aber einen Unterschied von 1,2 t/ha. Die Wahrscheinlichkeit ist gering, nämlich nur zehn Prozent, dass dieses Ergebnis von 1,2 t/ha eintritt, wenn die Hypothese zutrifft. Was folgern wir aus unserem Ergebnis von p=0,1. Wir schließen aus der geringen bedingten Wahrscheinlichkeit, dass wir unsere Hypothese vielleicht verwerfen sollten. Doch dazu später.
Nehmen wir an, der Unterschied zwischen den Gruppen würde nur 0,3 t/ha betragen und der Signifikanztest ergibt den Wert 0,8. Was heißt das? Wenn die Hypothese zutrifft, treten die tatsächlich ermittelten Daten von 0,3 t/ha mit einer Wahrscheinlichkeit von 80 Prozent auf. Der Signifikanztest legt uns also nahe, dass die Hypothese zutrifft, denn die ermittelten Daten legen das nahe. Auch wenn es langweilig werden sollte, werden wir das Obige wiederholen. Es ist sehr wichtig, dass wir es wirklich wirklich verstehen. Wir haben also auf der einen Seite unsere Daten. Diese werden beim Test nicht in Frage gestellt. Fakten sind Fakten. Es geht auch nicht um die Wahrscheinlichkeit der Fakten. Da Fakten sind, was sie sind. Sie sind sie es zu 100 Prozent! Auf der anderen Seite berechnen wir, wie wahrscheinlich die gemessenen Daten auftreten, wenn die Hypothese zutrifft. Da der Unterschied von 0,3 t/ha gering ist und die unterstellte Hypothese behauptet, dass kein Unterschied besteht, ist die Wahrscheinlichkeit natürlich sehr hoch, dass so geringe Unterschiede auftreten. Beträgt der Unterschied 5,2 t/ha und der p-Wert 0,01, dann ist es unwahrscheinlich (1 Prozent), dass genau dieses Ergebnis eintritt. In diesem Fall würden wir uns zu Recht gegen die Hypothese entscheiden.
Betrachten wir das Ganze noch einmal aus einem anderen Blickwinkel. Nehmen wir an, wir wollen wissen, wie viel Prozent der Frauen über 25 Jahre in einer Stadt Zentralasiens größer sind als 165 cm. Wir ziehen eine Stichprobe und stellen fest, dass es 40 Prozent sind. Am nächsten Tag wird eine weitere Stichprobe gemessen und es sind 42 Prozent, und am darauffolgenden Tag sind es 39 Prozent. Was schließen wir daraus? Wir stellen die Hypothese auf, dass ungefähr 40 Prozent der Frauen größer sind als 165 cm. Wie wahrscheinlich dürfte es in dieser Stadt sein, in einer vierten oder fünften Stichprobe nur bei zehn Prozent oder bei 80 Prozent eine Körpergröße über 168 cm festzustellen. Die Wahrscheinlichkeit dürfte gering sein, wenn die Hypothese der Realität entspricht. Je weiter die Werte von 40 Prozent abweichen, umso unwahrscheinlicher werden sie auftreten.
Jetzt nehmen wir diese Hypothese, kehren nach Deutschland zurück und testen dort dieselbe Hypothese, indem wir die Körpergröße in unserer Stadt bestimmen. Dabei stellen wir fest, dass bei uns 90 Prozent aller gemessenen Personen größer sind als 165 cm. Unter der Hypothese, dass Frauen zu 40 Prozent größer sind als 165 cm, ist die Wahrscheinlichkeit für unser Ergebnis sehr gering. Der p-Wert des Signifikanztestes beträgt 0,001. Solche Werte würden unter der obigen Hypothese nur in 0,1 Prozent auftreten. Also können wir folgern, dass die Hypothese nicht zutrifft und Frauen in Deutschland größer sind als in der asiatischen Stadt. Wir würden hier eher die Hypothese aufstellen, dass die Frauen in unserer Stadt größer sind als in der asiatischen Stadt.
Doch nun zurück zu unserem Landwirt, der endlich wissen wollte, ob er den Dünger kaufen soll oder nicht. Gemeinsam mit dem Hersteller des Düngemittels und einem Statistiker planten sie eine weitere Studie. Um die Unwägbarkeiten bei den vielfältigen Einflussgrößen gleichmäßig zu verteilen, teilten sie die Felder in 1000 Doppelquadrate ein. Jeweils eines der Quadrate wurde gedüngt und das andere nicht. Durch diese zufällige Zuordnung kleinerer Felder sollten die Verzerrungsmöglichkeiten weiter eingeschränkt werden. Zusätzlich wurde vor dem Versuchsbeginn vereinbart, wie die Daten auszuwerten sind. Dazu wurde jeweils ein Doppelquadrat analysiert. Die Ernte des gedüngten und des ungedüngten Anteils wurde betrachtet und die Differenz pro Doppelquadrat berechnet. Die Hypothese lautete, dass kein Unterschied zwischen gedüngten und ungedüngten Feldern besteht. Demnach müsste die Differenz bei null liegen. Insgesamt betrug die Differenz nach der Ernte aber auf allen Anteilen zusammen 2,2 t/ha. Der Signifikanztest ergab p=0,001. Der Landwirt war nun vom positiven Effekt des Düngers überzeugt und setzt ihn seitdem regelmäßig ein.

Abb. 9-3 Randomisierte Parzellierung
War diese Entscheidung richtig? Ja und Nein. Es war richtig, zu behaupten, dass der Dünger die Ernte verbessert. Der Signifikanztest zeigt in dieser Studie eindeutig, dass der Dünger die Ergiebigkeit erhöht, denn die Wahrscheinlichkeit, eine Differenz von 2,2 t/ha unter der Annahme der Hypothese zu erreichen, ist mit 0,1 Prozent sehr gering. Der Signifikanztest ist aber nicht alles. Wir erwähnten bereits, dass er häufig überschätzt wird. Der Test sagt uns nämlich nicht, wie relevant der Unterschied ist. In unserem Beispiel wurde vom Landwirt nämlich übersehen, dass den Mehreinnahmen durch die höhere Ernte von 2,2 t/ha die Kosten des Düngers gegenüberstehen. Und kosteneffektiv wäre es nur geworden, wenn er mindestens 2,8 t/ha mehr ernten würde. Dünger zu verwenden, kostet ihm letztlich mehr, als er einnimmt. Deshalb ist es falsch, unter diesen Bedingungen zu düngen. Ein signifikanter Unterschied bedeutet nicht zwangsläufig, dass der Unterschied auch wirklich relevant ist. Neben dem p-Wert des Signifikanzwertes sollten wir auch immer auf den tatsächlichen Unterschied schauen, um gute Entscheidungen zu treffen.