Kurioses
5. Kurioses
In diesem Kapitel werden wir uns mit kuriosen Zusammenhängen beschäftigen, die auf den ersten Blick etwas seltsam wirken. Nachdem wir die Zusammenhänge dann aber analysiert und geklärt haben, können wir die neuen Erkenntnisse gewinnbringend einsetzen.
5.1 Will-Rogers-Phänomen
Stellen wir uns vor, dass wir einem alten Freund bei einem wissenschaftlichen Regionalkongress begegnen. Unser Freund war direkt nach dem Medizinstudium ins Management einer kleinen Firma für Verbandsmaterial gewechselt. Mit den dortigen Erfahrungen stieg er sukzessive die Karriereleiter herauf, bis er nun im Controlling eines großen Krankenhauskonzerns tätig ist. Nachdem wir über alte Zeiten gelacht haben, seufzt er tief und fragt, ob wir ihm bei einem komplexen Problem helfen können. Da die Wörter „komplexes Problem“ bei uns sofort Helferimpulse freisetzen, hören wir ihm geduldig zu.
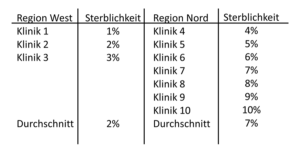
Es geht um die Sterblichkeit nach Operationen am Dickdarm. In seinem Konzern wird sehr viel Wert darauf gelegt, dass die Sterblichkeit nach Operationen niedrig ist – besonders im Vergleich zur Konkurrenz. Bei der Analyse der Regionen Nord und West stellte er fest, dass die durchschnittliche Sterblichkeit in den Regionen unterschiedlich hoch ist (Tab. 5-1) und höher als vom Konzern angestrebt. Sie betrug in der Region Nord neun Prozent und in der Region West vier Prozent. Die Anzahl der behandelten Patienten war in den Krankenhäusern beider Regionen vergleichbar.

Tab. 5-1 Sterblichkeit bei
zehn Kliniken eines Klinikkonzerns
Er wurde nun damit beauftragt, die Ursachen für die schlechten Ergebnisse herauszufinden und sie abzuschaffen. Dazu hatte er alle Kliniken aufgesucht und mit den dortigen Chefärzten die Fälle besprochen. Die Ärzte konnten alle Todesfälle plausibel erklären. Behandlungsfehler konnte er ebenfalls nicht feststellen. Insgesamt wurden von den Ärzten auch Verbesserungsvorschläge unterbreitet, von denen er sich aber keine deutliche Verminderung der Sterblichkeit versprach.Er zeigt uns seine Daten. Wir betrachten einige Zeit seine Ergebnisse und müssen laut lachen. Verdutzt schaut er uns an und fragt, warum wir denn über die Daten so schmunzeln müssen. Daraufhin sagen wir ihm, dass wir gerade an einen Witz des Cherookesen William Penn Adair Rogers denken müssen. Rogers wurde 1879 in Oklahoma geboren und war ein sehr bekannter Komiker und Kolumnist. In einem seiner Witze sagte er, „when the Okies left Oklahoma and moved to California, they raised the average intelligence level in both states.“
Da unser Freund uns weiterhin verständnislos ansieht, fragen wir ihn, wie weit er denn die Sterblichkeit vermindern solle. Seiner Meinung nach wäre eine Verringerung um 1 Prozent sicherlich schon als großer Erfolg zu bewerten. Wir rechnen ein bisschen herum und fragen ihn dann, was er uns als Beraterhonorar zahlen würde, wenn wir ihm eine Verminderung der Sterblichkeit um ca. zwei Prozent versprechen würden. Völlig ungläubig verspricht er uns eine Kiste Rotwein, die wir dankend annehmen, denn die durchschnittliche Sterblichkeit können wir vermindern, ohne an den aktuellen Ergebnissen der einzelnen Kliniken etwas ändern zu müssen. Wir nutzen nur das Will-Rogers-Phänomen und „schicken Okies nach Kalifornien“.Die Lösung ist letztlich ganz einfach und basiert auf einer geschickten Umgruppierung. Aus der Tab. 5-1 können wir ersehen, dass die Kliniken (1-7) der Region West jeweils eine Sterblichkeit von 1-7 Prozent aufweisen (zur Veranschaulichung wurden den Kliniken diese Prozentangaben zugewiesen). Im Durchschnitt beträgt die Sterblichkeit damit vier Prozent. In der Region Nord haben die drei Kliniken (8-10) eine höhere Sterblichkeit von 8-10 Prozent. Hier liegt sie im Durchschnitt bei neun Prozent. Um die Sterblichkeit zu vermindern, werden die Kliniken in den Regionen neu sortiert (Tab. 5-2).
Tab. 5-2 Sterblichkeit bei
zehn Kliniken eines Klinikkonzerns
nach Umgruppierung
Die Kliniken 4-7 sind die schlechten aus der alten Region West. Sie werden jetzt der Region Nord zugewiesen. Damit verbessern sie zwangsläufig die Ergebnisse der deutlich schlechteren alten Region Nord. Jetzt beträgt die Sterblichkeit im Durchschnitt nur noch sieben Prozent statt neun Prozent. Die Region Nord hat sich jetzt statistisch (im Durchschnitt) verbessert, ohne dass sich die konkreten Ergebnisse der einzelnen Kliniken geändert haben. Diese Neueinteilung ist auch für die Kliniken 1-3 günstiger, die in der Region West verblieben sind. Sie waren nämlich die besten Kliniken und verbessern ihre Sterblichkeit von vier Prozent auf zwei Prozent. Die schlechteren Kliniken wurden ja in die nördliche Region geschoben.
Wir schauen in die ungläubigen Augen unseres Freundes. Er ist völlig verblüfft, dass wir, ohne die Ergebnisse der einzelnen Kliniken zu tangieren, die Durchschnittswerte verändern können, indem wir einfach die Kliniken umgruppieren. Auf die Frage unseres Freundes, woher wir das alles wissen, verweisen wir auf das Will-Rogers-Phänomen und seinen oben zitierten Witz. Solche Effekte können nämlich immer dann auftreten, wenn Mittelwerte über Gruppen gebildet werden und vereinzelte Elemente die Zugehörigkeit wechseln. Der Witz unterstellt zwei Annahmen: Erstens müssen die Kalifornier einen niedrigeren IQ haben als die Bewohner Oklahomas und zweitens müssen die Okies die relativ „dummen“ Bewohner Oklahomas sein. Nur wenn beide Bedingungen erfüllt sind, dann erhöht sich der IQ in beiden Ländern. Letztlich wollte Rogers mit diesem Witz auf die wenig intelligent Kalifornier hinweisen.
In der Medizin tritt dieses Phänomen relativ häufig auf. Am bekanntesten ist es als „Stadienmigration“ bei Tumoren bekannt. Diese Abhängigkeiten sollten wir verstehen, um uns nicht von angeblich besseren Behandlungsverfahren oder Operationen blenden zu lassen, die in Wirklichkeit nur dem Will-Rogers-Phänomen zu verdanken sind.Wir teilen zum Beispiel bösartige Tumoren in vier Stadien ein (Tab. 5-3).
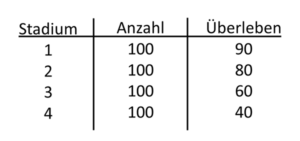
Tab. 5-3 Stadien eines Tumors
und die Überlebensrate
Je höher das Stadium, je fortgeschrittener der Tumor desto schlechter das Überleben. Wir haben der Einfachheit wegen festgelegt, dass in jedem Stadium 100 Patienten enthalten sind.Nehmen wir jetzt hypothetisch an, dass wir das Operationsverfahren verändern. Statt der üblichen kleinen Operation führen wir jetzt eine ausgedehnte radikale Operation durch. Wir bezwecken durch die radikale Operation ein verbessertes Überleben. Und siehe da, nachdem wir 400 Patienten operiert haben, haben sich die Überlebenszeiten in allen Stadien gebessert (Tab. 5-4). Wie können wir uns das erklären? Die Anhänger der radikalen Operation werden sagen, dass es an den ausgedehnteren Operationen liegt, die die Überlebenschance verbessern. Die Kritiker der radikalen Operation werden behaupten, dass es nur zu einer Migration von Patienten gekommen ist.
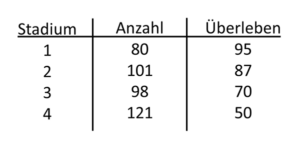
Tab. 5-4 Stadien eines Tumors
und die Überlebensrate nach
zusätzlicher radikaler Operation
Betrachten wir dazu das Stadium 1. Wenn wir ausgedehnter operieren, dann werden wir durch die umfangreichere feingewebliche Untersuchung feststellen, dass einige Patienten, die früher dem Stadium 1 zugeordnet waren, doch nicht mehr zu diesem Stadium gehören, sondern bereits zum Stadium 2. Die „gründlichere“ Untersuchung bei den ausgedehnteren Operationen verschiebt die Patienten in höhere Stadien. Da wir guten Gewissens unterstellen können, dass gerade diese Patienten eine etwas schlechtere Prognose haben, verbessert die Migration zwangsläufig die Prognose im Stadium 1, weil die „Besseren“ dort verbleiben, und auch im Stadium 2, weil dort die „Besseren“ hinzukommen. Denselben Mechanismus können wir getrost für alle Stadien unterstellen, so dass sich die Prognose in allen Stadien verbessert. Die Patientenzahl verschiebt sich natürlich insgesamt in fortgeschrittene Stadien. Diese Migration basiert darauf, dass die einzelnen Stadien durch die bessere Untersuchung exakter zugeordnet werden können.Wie können wir diesem Phänomen entgehen? Wir könnten durch vergleichende Studien überprüfen, ob ein Verfahren tatsächlich besser ist. Wir könnten aber auch das Gesamtergebnis berechnen. Das Gesamtergebnis ändert sich nämlich durch die alleinige Umverteilung nicht. Wenn wir in dem obigen Beispiel aus den Regionen West und Nord alle Sterblichkeiten berücksichtigen, dann sind sie vor und nach der Umgruppierung identisch.
Der Effekt tritt auch andersherum ein. Wenn zum Beispiel eine gut strukturierte chirurgische Klinik eine kurze Verweildauer aufweist und eine internistische Klinik eine längere Verweildauer, dann können sich beide durchschnittliche Verweildauern verlängern, ohne dass sich konkret irgendetwas verändert hätte. Wenn nämlich der Internist seine „schnellsten und besten“ Fälle in die Chirurgie verlegt. Sie bleiben dann aus der Berechnung der internistischen Verweildauer außen vor. Die durchschnittliche Verweildauer verlängert sich somit beim Internisten. Der Chirurg hat jetzt mehr „Langlieger“ und dadurch verlängert sich seine Liegedauer ebenfalls. Diese Verschiebungen treten in den durchschnittlichen Verweildauern der einzelnen Kliniken auf, die dann möglicherweise vor den Verwaltungsleitern der Kliniken unsinnigerweise gerechtfertigt werden müssen.
5.2 Simpson Paradox
Das Simpson Paradox wird nach dem Statistiker Edward Hugh Simpson benannt. Es kann immer dann auftreten, wenn wir Ergebnisse von Gruppen miteinander kombinieren. Das klingt zunächst harmlos. Ein konstruiertes Beispiel soll uns mit dem Problem vertraut machen.
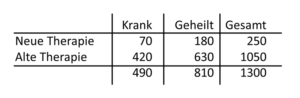
Tab. 5-5 Therapie in der Klinik A
Stellen wir uns vor, wir führen eine neue Therapie zur Behandlung von Rückenschmerzen ein und vergleichen sie mit der alten Therapie (Tab. 5-5). In der Klinik A sind wir bei 180/250 bzw. 72 Prozent mit der neuen Methode erfolgreich und nur bei 630/1050 bzw. 60 Prozent mit der alten Methode.
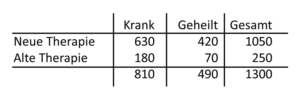
Tab. 5-6 Therapie in der Klinik B
Enthusiastisch empfehlen wir das neue Verfahren nun der befreundeten Klinik B, die nach einem Jahr ihre Ergebnisse präsentiert (Tab. 5-6). Hier ist die neue Therapie nicht ganz so erfolgreich mit 420/1050 bzw. 40 Prozent. Aber die alte Therapie ist auch hier eindeutig schlechter mit 70/250 bzw. 28 Prozent.
Nachdem wir unser neues Verfahren bei sehr vielen Patienten getestet haben und es in beiden Kliniken besser abschneidet als das herkömmliche Verfahren, schreiten wir zu einer Presseerklärung und Publikation. Die Zeitschrift verlangt von uns, die Ergebnisse in einer einzigen Tabelle zusammenzufassen (Tab. 5-7) Und jetzt kommt der Clou. Die neue Therapie ist nur bei 600/1300 erfolgreich und die alte Therapie bei 700/1300. Plötzlich ist die alte Therapie besser und nicht die neue.
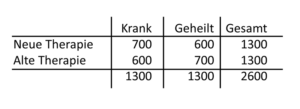
Tab. 5-7 Therapie in beiden Kliniken
Wie kann das sein? Wo ist der Fehler? Beruht alles nur auf unserer Konstruktion oder tritt so etwas auch real ein.Letztlich beruht der Effekt darauf, dass eine bestimmte Gruppe in der einen Klinik unterrepräsentiert und in der anderen Klinik überrepräsentiert ist. Dadurch entstehen Fehler in der Zusammenstellung der Daten.Das wahrscheinlich berühmteste Beispiel des Simpson Paradoxon ist die Diskriminierungsklage gegen die Berkely Universität in Kalifornien. Es wurde damals eine Übersicht veröffentlicht, wie viel Prozent der Frauen und Männer an der Universität abgelehnt wurden. Aus dieser Übersicht wurde vermeintlich nachgewiesen, dass die Aufnahmequote der Frauen im Herbst 1973 niedriger war als die der Männer. Bei genauerer Analyse offenbarte sich aber eine Ungleichverteilung der Frauen in den verschiedenen Bereichen. Frauen bewarben sich besonders dort, wo es nur wenig offene Stellen gab, die nicht sehr viele Studenten aufnahmen. Männer entschieden sich dagegen für Fächer, die nicht so überlaufen waren. Durch diese ungleiche Verteilung entstand ein völlig falscher Eindruck.
Wenn wir ungleiche Verteilungen von relevanten Eigenschaften wie Geschlecht oder Alter in Häufigkeiten erkennen, dann sollten wir uns dieses Paradoxons bewusst sein und getrennte Analysen für die einzelnen Gruppen vornehmen. Es könnte dann sein, dass sich die Aussagen völlig verändern, wenn wir die gesamte Population betrachten oder die jeweiligen Untergruppen.
5.3 Regression zur Mitte
Nehmen wir an, dass drei Personen unserer Familie an einer schweren Grippe erkranken. Nachdem wir einige Tage alle häuslich verfügbaren Mittel eingenommen haben und die Körpertemperatur dennoch ansteigt (Fieber), lassen wir uns ärztlich behandeln, allerdings jeder von einem anderen Arzt. Der erste Arzt verschreibt ein Grippemittel A, der zweite ein homöopathisches Präparat B zum Selbstbezahlen und er dritte verzichtet vollständig auf Medikamente, weil die Krankheit nach Meinung des Arztes schon fast überwunden scheint. Einige Tage später geht es uns allen besser, so dass die Wirkung des Medikamentes A und des homöopathischen Präparates B fraglich erscheint. Wie können wir uns die Besserung erklären?
Wir lesen heute Morgen in der Zeitung, dass die Rentenversicherungen ein neues Konzept für die Rehabilitation von Arbeitsunfähigen eingeführt haben, das nachweislich sehr erfolgreich sein soll. Sie rehabilitierten Personen, die in den letzten Jahren sehr häufig arbeitsunfähig waren. Nach zwei Jahren verglichen sie die speziell behandelten Personen mit den anderen Versicherten und stellten fest, dass die Häufigkeit der Arbeitsunfähigkeit in der behandelten Gruppe abgenommen hat. Ist damit der Erfolg des neuen Konzeptes hinreichend belegt oder könnten auch noch andere Faktoren dafür verantwortlich sein?
In beiden Beispielen könnte der nachweisbare Effekt ausschließlich auf ein zufälliges Phänomen zurückgeführt werden, welches „Regression zur Mitte“ genannt wird. Es basiert auf einer Beobachtung von Francis Galton, der im 19. Jahrhundert die vererbbare Größe von Erbsen untersuchte. Später ergänzte er seine Vermutung und bestätigte sie an der Körpergröße von Menschen. Galton stellte fest, dass Gruppen, deren Merkmalsausprägungen stark erhöht oder stark erniedrigt waren, dazu tendieren, sich im Laufe der Zeit wieder zum Durchschnitt zu entwickeln. Sehr große Menschen erzeugen keine Kinder, die ebenfalls wieder sehr groß oder noch größer werden. Das würde nach einigen Generationen zu Riesen führen. Es ist vielmehr so, dass die großen Eltern zwar wieder große Kinder bekommen, aber diese sind etwas kleiner und tendieren damit wieder zum Durchschnitt. Ähnlich verhält es sich auch bei den kleinen Personen.Diese „Regression zur Mitte“ betrifft nur die Tendenz der extremen Merkmalsträger. Nur wenn wir diese Gruppe betrachten, stellen wir den Effekt fest. Betrachten wir dagegen die gesamte Bevölkerung, dann ändert sich nichts an der Verteilung, weil natürlich auch durchschnittlich große Personen größere oder kleinere Kinder bekommen. Diese „Regression zur Mitte“ bedeutet nicht, dass nach einer gewissen Zeit alles zum Durchschnitt tendiert.
Nun zurück zu unseren Beispielen. Wenn wir unsere Grippe bereits anbehandelt haben und nun bei der quasi „maximalen“ Verschlechterung zum Arzt gehen, dann wird es auf jeden Fall besser, egal was wir tun. Unter solchen Situationen „wirken“ alle Maßnahmen gleichermaßen gut. Sollte sich ein homöopathisches Präparat als besonders nebenwirkungsarm auszeichnen, dann sollten wir die „Regression zur Mitte“ ausschließen, bevor wir dem Präparat eine eigenständige Wirkung zuschreiben. Das zweite Beispiel ist noch einleuchtender. Wenn wir nämlich bei den Arbeitsunfähigen von vornherein nur die Gruppe betrachten, die sehr häufig krank ist, dann wird auch hier zwangsläufig die Häufigkeit der Arbeitsunfähigkeit abnehmen. Aber nicht aufgrund der erfolgreichen und teuren Rehabilitationsprogramme, sondern allein schon wegen der „Regression zur Mitte“. Umgekehrt könnten wir wahrscheinlich auch bei den „immer“ Gesunden nachweisen, dass sie häufiger krank werden. Beide Extreme, häufig krank oder immer gesund sein, streben zur Mitte. Genauso wie durchschnittliche Personen in die Extreme driften können. Solange sich die „Regression zur Mitte“ und der „Drang zum Extremen“ die Waage halten, ändert sich der durchschnittliche Wert nicht. Deshalb werden wir auch nicht zu Riesen oder Zwergen, sondern pendeln uns stabil bei einer bestimmten Körpergröße ein, die allerdings gering zuzunehmen scheint.
Sollten wir also einmal krank werden und mit Fieber zum Arzt, Apotheker, Heilpraktiker oder Wunderheilern gehen, dann können wir eigentlich sicher sein, dass eine Besserung eintreten wird. Inwieweit die durchgeführte Therapie tatsächlich den Krankheitsverlauf positiv beeinflusste, bleibt ungewiss. Nur überprüfbare Studien können die „Regression zur Mitte“ ausschließen.