Numerische Werte
4. Numerische Werte
Da wir seit der Grundschule über fundierte Kenntnisse der Grundrechenarten verfügen, fühlen wir uns ausreichend gewappnet, um nach Wegen zu suchen, unübersichtliches Zahlenmaterial verständlich aufzubereiten, so dass die Ergebnisse für andere nachvollziehbar werden. Das mag zwar auf den ersten Blick banal erscheinen, aber es ist doch nicht ganz so einfach, wie wir noch sehen werden.

Tab. 4-1 Alter der Geburtstagsgäste
Stellen wir uns eine Geburtstagsparty vor, zu der wir eingeladen sind. Es ist langweilig, wir sitzen auf dem Sofa und fragen uns, wie alt die Gäste sind. Wenn nur fünf andere Personen anwesend sind, können wir uns rasch eine Übersicht verschaffen, indem wir jedes Alter aufzählen. Und wenn wir ein schlechtes Gedächtnis haben, zücken wir unser Smartphone und legen eine Tabelle an. Bei zwanzig Gästen wird es schon unübersichtlicher und bei fünfzig oder hundert Gästen werden wir uns kaum auf unsere Gedächtnisleistung verlassen. Jetzt sind spätestens elektronische Hilfsmittel erforderlich, um die Daten zu speichern und aufzuarbeiten. Speichern allein und in einer Tabelle auflisten, wird nicht ausreichen, um uns eine Übersicht zu verschaffen. Selbst wenn wir 100 Zahlen als Zahlenkolonne untereinander schreiben, werden die Daten nicht übersichtlicher. Was wir benötigen, sind zusätzliche Kennzahlen, die die Daten von 50, 100 oder noch mehr Personen verständlich zusammenfassen bzw. repräsentieren. Diese Kennzahlen sollen uns zwei Informationen vermitteln: Welcher Wert liegt ungefähr in der Mitte (Lagemaße) und wie sind die Werte insgesamt gestreut (Streuungsmaße)? Erst beide Maße zusammen gestatten uns eine ausreichende Übersicht, um die Daten zu verstehen, einzuordnen und zu interpretieren. Gegen diese Einsicht, dass wir immer beide Maße benötigen, wird leider häufig verstoßen – manchmal aus Unwissenheit und manchmal, um Andere zu täuschen.
4.1 Mittelwert und Median
Beginnen werden wir mit den Lagemaßen, denn mit ihnen können wir uns daran orientieren, wo ungefähr die Mitte der Werte liegt. Als die beiden wichtigsten Lagemaße gelten der (arithmetische) Mittelwert und der Medianwert. Es gibt noch weitere (geometrischer und harmonischer Mittelwert, Modalwert), die jedoch nur für besondere Fragestellungen wichtig sind, sowie das Minimum und Maximum, die für sich selbst sprechen. Am häufigsten wird sicherlich der Durchschnittswert bzw. Mittelwert verwendet. Auf unserer Geburtstagsparty können wir nun leicht ausrechnen, wie hoch das Durchschnittsalter aller Gäste ist. Dazu addieren wir das Alter aller Gäste und dividieren es durch die Anzahl der Gäste. Dieses ist eine sehr einfache Rechnung. Bei der Feier meines Opas betrug das Durchschnittsalter 73 Jahre und bei meiner Tochter 18 Jahre (Tabelle 4-1), was nicht weiter verwunderlich ist. Wir können mit dem leicht berechenbaren Durchschnitt verschiedene Gruppen vergleichen und behaupten, dass die Teilnehmer in der einen Gruppe älter waren als in der anderen.

Tab. 4-2 Jahreseinkommen einer Gemeinde
Wir könnten zum Beispiel berechnen, wie hoch das Durchschnittseinkommen der einzelnen Haushalte in verschiedenen Stadtteilen einer Großstadt ist und könnten dann „reiche“ und „arme“ Stadtteile identifizieren. In öffentlichen kommunalen Statistiken werden solche Angaben regelmäßig angeführt. Wenn wir eine beliebige Zeitung aufschlagen, dann werden wir fast immer Zahlenmaterial finden, das Durchschnittswerte enthält und diese Werte zwischen Gruppen vergleicht.
Diesen Durchschnittswerten dürfen wir keinesfalls blind vertrauen, selbst wenn die Daten korrekt erhoben wurden und die Berechnung fehlerfrei ist. Immer dann, wenn uns ein Durchschnittswert als einzige verlässliche Zahl angeboten wird, sollten wir auf der Hut sein, denn der Sinn und Unsinn von Durchschnittswerten hängt von anderen wichtigen Faktoren ab, die bekannt sein müssen – ansonsten können wir die Durchschnittswerte nicht richtig interpretieren und Fehleindrücke sind häufig, ja manchmal sogar bewusst beabsichtigt. Nehmen wir dazu noch einmal die Daten unserer beiden Geburtstagsfeiern. Wir könnten behaupten, dass die Gäste bei den beiden Feiern durchschnittlich 45,5 Jahre alt waren. Diese Information ist vollkommen korrekt, aber eigentlich nur falsch interpretierbar. Die ausschließliche Angabe eines Lagemaßes kann uns so richtig in die Irre führen.

Nehmen wir nun an, wir wollen das jährliche Durchschnittseinkommen einer kleinen Gemeinde berechnen. Die Gemeinde besteht aus zehn Haushalten, deren Einkommen tabellarisch aufgelistet ist (Tabelle 4-2). Das gesamte Einkommen aller Haushalte beträgt 600.000 €. Bei zehn Haushalten entspricht das durchschnittliche Einkommen demnach 60.000 €. Wenn wir nun im Gemeindeblatt veröffentlichen würden, dass das Einkommen pro Haushalt 60.000 € beträgt, dann würden wir wahrscheinlich Schmähbriefe von 80 Prozent der Haushalte bekommen, denn diese verfügen über deutlich weniger als 60.000 €. Offensichtlich drückt der Durchschnittswert nicht das aus, was wir uns vorgestellt haben. Die beiden sehr hohen Einkommen scheinen den Wert so zu verzerren, dass er uns den falschen Eindruck vermittelt, die Gemeindemitglieder würden ungefähr 60.000 € verdienen.
Nehmen wir als weiteres Beispiel an, dass der Haushalt mit dem höchsten Einkommen umzieht und bei der nächsten Berechnung unberücksichtigt bleibt. Jetzt beträgt das gesamte Einkommen nur noch 200.000 €, das nun durch neun Haushalte geteilt werden muss. Das durchschnittliche Einkommen beträgt jetzt nur noch 22.222 €. Wir erkennen, dass ein einziger Haushalt das durchschnittliche Einkommen fast verdreifacht hatte. Bei der Berechnung von Durchschnittswerten können extreme Werte starken Einfluss auf das Gesamtergebnis nehmen, so dass Durchschnittswerte ohne weitere Angaben über die eigentliche Werteverteilung sehr problematisch sind. Wir unterstellen nämlich immer, dass die Werte relativ nah um den Durchschnittswert schwanken oder dass die extremen Werte auf beiden Seiten gleich häufig sind. Sind diese Bedingungen nicht erfüllt, dann vermittelt uns der Mittelwert einen trügerischen Eindruck – er kann richtig sein oder auch richtig falsch!
Ein weiteres extremes Beispiel soll uns niemals vergessen lassen, wie problematisch die alleinige Angabe von Mittelwerten ist. Stellen wir uns vor, dass einer der Albrecht-Brüder (Aldi) mit einem geschätzten Vermögen von 15 Milliarden Euro und einem spekulativen Einkommen von 100 Millionen Euro im Jahr ein Haus in dieser Gemeinde bezieht. Das jährliche Einkommen würde sich dann auf 100.600.000 € erhöhen, was einem ungefähren durchschnittlichen Einkommen pro Haushalt von 10.000.000 € entspräche. Niemand würde aber ernsthaft behaupten wollen, dass alle Gemeindemitglieder Einkommensmultimillionäre sind. Diese Beispiele sollen uns ermahnen, niemals irgendwelchen Durchschnittsgrößen zu glauben. Sie sind häufig die einzigen Werte, die im populären Bereich veröffentlicht oder genannt werden. Und sie werden verwendet, um sowohl faire als auch unfaire Vergleiche zu ziehen. Wenn uns nicht zusätzlich die Verteilung der Daten mitgeteilt wird, sind Mittelwerte problematisch und nur unter Vorbehalt interpretierbar.

Was würde sich für eine andere Kennzahl anbieten, wenn wir uns einen verlässlichen Eindruck über das „mittlere“ Einkommen verschaffen wollten. Am besten wäre es, wenn wir die Einkommen der Reihenfolge nach ordnen, wie bereits in der Tabelle 4-2 geschehen, und dann einfach schauen, welcher Wert sich in der Mitte befindet. Dieser Wert in der tatsächlichen und nicht berechneten Mitte wird „Medianwert“ genannt. Er ist ein verlässlicheres Maß als der Mittelwert, denn die extremen Werte haben auf ihn keinen Einfluss. In unserem Beispiel liegt der Median zwischen den beiden Werten 20 000 € und 25 000 €, so dass der Median 22 500 € entspricht. Obgleich der Median dem Mittelwert sicherlich vorzuziehen ist, wird der Mittelwert gern gewählt, weil er sich sehr viel leichter in Computerprogrammen berechnen lässt.
4.2 Standardabweichung
Wozu benötigen wir überhaupt noch Streuungsmaße, wenn wir doch schon wissen, wo die Durchschnittswerte liegen? Betrachten wir noch einmal die beiden Geburtstagsfeiern meines Großvaters und meiner Tochter, die wir beide zusammengefasst hatten. Auch hier ist der Median allein nicht der Weisheit letzter Schluss, denn er liegt zwischen 66 und 20 Jahren. Er beträgt somit (66+20)/2=43 Jahre und unterscheidet sich kaum vom Mittelwert. Die Lagemaße von durchschnittlich 45,5 Jahren oder einem Median von 43 Jahren würden die verzwickte Situation nicht aufdecken, dass wir eine junge und eine ältere Gruppe zusammengefasst haben. Dazu sind nur Streuungsmaße fähig.

Eine kleine Geschichte wird die Notwendigkeit von Streuungsmaßen weiter stützen: „Als Herr Schmidt eines Tages nach Hause kommt, begrüßte ihn sein fünfjährige Tochter mit den freudigen Worten: „Wir haben die Meerschweinchen gemessen“. Sie zerrt ihn in die Küche, wo seine siebenjährige Tochter und seine Frau gerade beim Füttern von zwei Meerschweinchen sind. Auf seine Frage, worum es gehe, sagt ihm seine Frau, dass sie alle gemeinsam das Gewicht des jüngeren Meerschweinchens gemessen hätten, weil sie befürchteten, dass es zu wenig frisst und abnimmt. Zur Messung des Körpergewichtes hatten sie eine kleine zehn Zentimeter durchmessende Küchenwaage verwendet, auf der sie eine kleine Plastikschüssel gelegt hatten. Das Meerschweinchen wurde dann in die Plastikschüssel gesetzt. Natürlich gegen den Widerstand des Meerschweinchens. Seine Frau erhob den ersten Messwert mit 950 Gramm. Da sie seine Einstellung gegenüber Messwerten kannte, wiederholte sie den Versuch zwei weitere Male. Die Werte betrugen 940 g und 960 g. Also wurde der Durchschnitt der drei Messwerte berechnet: 950 g. Angeregt von ihrer Mutter wollte die älteste Tochter ebenfalls das Meerschweinchen wiegen. Die drei etwas holprigen Messungen ergaben: 850, 950 und 1050 g. Die Mutter berechnete den Mittelwert dieser Messungen. Er betrug ebenfalls 950 g und die Tochter war sehr stolz, weil sie dasselbe Gewicht gemessen hatte. Daraufhin versuchte es die eher stürmische jüngste Tochter. Beim ersten Mal quiekte das Tier etwas, weil es aus der Schale springen wollte. Es wurde aber in der Schale festgehalten und die Messung erbrachte 1650 g. Bei der zweiten Messung wurde das Tier aus Vorsicht etwas angehoben, so dass es nur noch 250 g wog. Beim dritten Messen ging offensichtlich alles glatt, denn jetzt wog das Tier 950 g. Auch die jüngste Tochter bestand auf die Berechnung des Mittelwertes und siehe da, er betrug ebenfalls 950 g. Daraufhin waren alle sehr stolz, das Gewicht des Tieres verlässlich gemessen zu haben.“
Wenn wir nur die Durchschnittswerte kennen würden, dann könnten wir behaupten, dass bei allen drei Messungen derselbe Messwert erhoben wurde und es offensichtlich nicht bedeutsam ist, wer die Messung vornimmt. Da wir aber die Streuung der Ergebnisse kennen, würden wir der jüngsten Tochter sicherlich weniger vertrauen, wenn sie nach zwei Wochen das Gewicht kontrolliert.
Wenn wir die Streuung der Daten kennen, dann wissen wir, wie nahe die anderen Ergebnisse um den Mittelwert oder Median variieren. Diese Information ist sehr wichtig, denn wenn die Streuung sehr groß ist, dann könnte das nächste Ergebnis vom Mittelwert stark abweichen. Die Streuung können wir einfach als Bereich zwischen dem Minimum und Maximum angeben.

Abb. 4-1 Prinzipien eines Box-and-Whisker-Plots
Dann wüssten wir zwar die gesamte Spannbreite der Werte, aber sie könnte durch Ausreißer nach unten oder oben deutlich verzerrt sein. Dem können wir ausweichen, wenn wir nicht die vollständige Spannbreite angeben, sondern den Bereich zwischen der 5-%- und der 95-%-Perzentile. Lassen wir uns nicht durch den Ausdruck „Perzentile“ verschrecken. Nehmen wir an, wir haben 500 Werte erhoben. Wenn wir alle Werte ihrer Reihenfolge nach ordnen, dann liegen die 25 höchsten Werte (5 Prozent) oberhalb der 95-%-Perzentile und die 25 niedrigsten Werte unterhalb der 5-%-Perzentile. Mögliche extreme Ausreißer, die bei jeder Messung auftreten können, liegen dann außerhalb dieses Bereichs und erregen damit weniger Aufmerksamkeit. Glücklicherweise übernehmen heutzutage Computerprogramme die graphische Darstellung, so dass wir uns mit der Aufarbeitung der Daten nicht beschäftigen müssen.
Am häufigsten wird gemeinsam mit dem Mittelwert die Standardabweichung als Maß für die Streuung genannt. Beide gemeinsam sind die optimalen Kennziffern bei Daten, die normal verteilt sind. Was das genau heißt, werden wir später besprechen. Die beste graphische Abbildung numerischer Werte wird mit einem sogenannten Box-and-Whisker-Plot erreicht (Abb. 4-1). Diese Abbildungen sind heute als Goldstandard zu fordern. Lediglich bei wenigen Messwerten können sie durch die Einzelwerte ersetzt werden. Typischerweise wird beim Box-Plot der Median und/oder der Mittelwert als Querstrich in einem Rechteck gezeichnet. Der Median bildet exakt die Mitte aller Werte ab. Das Rechteck (Box) zeigt oben die 75-%-Perzentile und unten die 25-%-Perzentile. Innerhalb dieses Rechtecks liegen also 50 Prozent aller Werte. Nach oben und unten schließt sich ein Strich (Whisker) an, der wiederum in einen Querstrich übergeht. Der obere Querstrich zeigt die 95-%-Perzentile und der untere die 5-%-Perzentile. Zwischen beiden Abschnitten liegen also 90 Prozent aller Werte. Alle weiteren extremen Werte werden üblicherweise durch einzelne Punkte dargestellt.

Abb. 4-2 Mehrere Box-Plots
Exemplarisch werden vier Box-Plots gezeigt (Abb. 4-2). Im ersten und zweiten Box-Plot sind die Mittelwerte gleich, aber die Streuung verschieden. Im dritten Boxplot wird eine Population abgebildet, die sich deutlich von den vorigen beiden unterscheidet. Hier ist nicht nur der Mittelwert größer, sondern auch ein Großteil der Population zeigt höhere Werte. Im vierten Box-Plot werden der Mittelwert und Median gezeigt. Der Mittelwert, der sich nicht in der Mitte des Rechtecks befindet, weist auf eine schiefe, asymmetrische Verteilung der Daten hin.
Wir wollen an dieser Stelle auch die Gelegenheit nutzen, an dem Meerschweinchenbeispiel zu zeigen, welche zufälligen Schwankungen bei Messungen auftreten können. Natürlich erwarten wir, dass dieselben Messungen auch immer zu denselben Ergebnissen führen. Diese Anforderung ist einerseits trivial, wenn wir sie oberflächlich betrachten, und andererseits unerfüllbar, wenn wir etwas tiefer blicken. Exakt dieselben Messungen gibt es höchstens unter außergewöhnlichen experimentellen Bedingungen, weil die Ausgangsbedingungen genau übereinstimmen müssten. Wenn wir im medizinischen Alltag wiederholte Messungen vornehmen, um einen Körperzustand zu bestimmen, dann schwanken die Messwerte zum Teil erheblich. Relativ ideale Bedingungen wären vielleicht gegeben, wenn wir dieselbe Blutprobe in sehr kurzer Zeit mehrfach überprüfen würden: wir nehmen Blut ab und bestimmen 20mal aus derselben Probe die Anzahl der roten Blutkörperchen. In dieser Situation würden wir Werte mit einer sehr geringen Streuung erwarten (Abb. 4-3).

Abb. 4-3 Zunehmende Variabilität verschiedener Populationen
Wenn wir aber bei einem Menschen in stündlichen Abständen zwanzig Blutproben entnehmen und die Anzahl der roten Blutkörperchen bestimmen würden, dann wäre eine kleine Schwankungsbreite normal. Würden wir bei demselben Patienten an zwanzig verschiedenen Tagen die roten Blutkörperchen messen, dann würden die Werte weiter schwanken – besonders wenn wir die Blutproben auch noch zu verschiedenen Tageszeiten entnehmen würden. Wenn wir bei einer 30jährigen Frau mit schweren Menstruationsblutungen ebenfalls zwanzig Blutproben innerhalb von vier Wochen untersuchen, dann schwanken die Werte erheblich. Wenn wir statt einer Person zwanzig verschiedene Personen in demselben Alter und desselben Geschlechtes analysieren, schwanken die Werte noch weiter. Messen wir bei beiden Geschlechtern und in allen Altersgruppen, nimmt die Variabilität weiter zu. Fassen wir jetzt auch noch die Gesunden und Kranken zusammen, dann erhalten wir die größte Schwankungsbreite. Diese variierende Schwankungsbreite erkennen wir sehr deutlich in den Box-Plots (Abb. 4-4).

Abb. 4-4 Zunehmende Variabilität
Wenn wir numerische Werte präsentieren, dann müssen wir ein Lagemaß mit einem Streuungsmaß kombinieren. Erst beide zusammen vermitteln uns eine adäquate Übersicht über die Daten. Wenn nur ein Lagemaß mitgeteilt wird, dann sind gravierende Fehlinterpretationen nicht auszuschließen. In wissenschaftlichen Publikationen sind beide Maße vorgeschrieben. Für numerische Werte hat sich der Box-Plot durchgesetzt, weil auf einen Blick alle relevanten Informationen sichtbar sind.
4.3 Normalverteilte Daten
Jetzt werden wir uns mit der „Normalverteilung“ beschäftigen.

Abb. 4-5 Das Lebensalter zum Zeitpunkt der Diagnose (n=50)
Was ist mit der Verteilung von Daten überhaupt gemeint? Betrachten wir dazu die folgende Liste, die das Lebensalter von 50 Patienten mit der Erstdiagnose eines Dickdarmkrebses notiert (Abb. 4-5). Diese Daten sind für uns nicht sinnvoll interpretierbar, weil die Daten zufällig verteilt sind und wir in ihnen kein Muster erkennen. In einem ersten Schritt werden wir nun die Daten der Reihenfolge nach sortieren und zusätzlich in Zehnjahresintervallen aufschreiben. Dazu verwenden wir eine Darstellungstechnik die sich Stamm-und-Blatt-Diagramm (Stem-and-Leaf) nennt (Abb. 4-6).

Abb. 4-6 Geordnete Lebensalter als Stamm-Blatt-Diagramm (n=50)
Auf der linken Seite sind untereinander die Zehnjahresintervalle angezeigt, die den Stamm darstellen. Vom Stamm geht dann jeweils das Alter innerhalb des Intervalls ab, ausgedrückt durch eine Zahl. Beide Zahlen ergeben das Alter. Wir erkennen jetzt auf einen Blick, dass die meisten Menschen zwischen 60 und 69 Jahren erkranken. In diesem Jahrzehnt werden am meisten Dickdarmkrebse diagnostiziert. Mit diesem Stamm-und-Blatt-Diagramm können wir uns auf einfache Art und Weise einen sehr guten Überblick über die Verteilung der Lebensalter machen. Wir erkennen Häufungen und in welchem Intervall nur wenige Menschen erkranken.
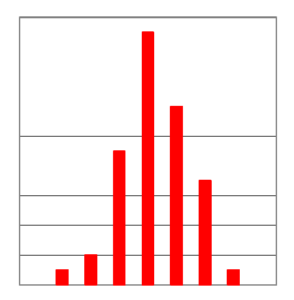
Abb. 4-7 Verteilung der Daten
Wenn wir jetzt das Stamm-und-Blatt-Diagramm um 90 Grad gegen den Uhrzeigersinn drehen, dann erhalten wir eine typische Verteilungskurve, wie wir sie aus den Lehrbüchern kennen (Abb. 4-7). Auf der x-Achse der Verteilungskurven sind quasi die Häufigkeiten in den einzelnen Intervallen abgebildet. Diese Verteilungskurven vermitteln uns auf einen Blick, wie die Daten verteilt sind. Die meisten Daten häufen sich um einen Mittelpunkt und werden dann auf beiden Seiten kontinuierlich seltener, je weiter sie von diesem Mittelpunkt entfernt sind. Wir können uns das so vorstellen, dass wir bei sehr vielen Messungen desselben Sachverhaltes nicht immer denselben Wert erhalten, sondern immer wieder kleinere oder größere Abweichungen.

Abb. 4-8 Normalverteilte Daten
Die kleinen Abweichungen sind natürlich häufiger als die seltenen größeren Abweichungen. Das Resultat ist bei sehr vielen Messungen eine typische Glockenkurve von gleichmäßig, symmetrisch verteilten Daten (Abb. 4-8), denn die Abweichungen nach links und rechts werden gleich häufig auftreten.
Bei 1000 Messungen, die normal verteilt sind, schwanken die Werte symmetrisch um einen Mittelwert, der bei der Abschätzung der Grundgesamtheit auch Erwartungswert (µ) genannt wird. Je nachdem, ob die Werte nur wenig um diesen variieren oder sehr stark variieren, wird die Glockenform eng oder weit. Erinnern wir uns an die zunehmende Variabilität von Messungen aus dem vorhergehenden Abschnitt. Hier ändern sich die Kurven von einem steilen, schmalen Bereich zu einen flachen, weiten Bereich.
Als Maß für die Variabilität der Daten gilt die Varianz, die bei normalverteilten Daten durch die Standardabweichung σ angegeben wird (Abb. 4-9). Wir dürfen uns nicht von den Begriffen „Varianz“ und „Standardabweichung“ erschrecken lassen. Varianz und Variabilität klingen schon einmal ähnlich und lassen sich dadurch gut merken. Die Varianz ist genau genommen die mittlere quadratische Abweichung der Daten vom Mittelwert. Die Standardabweichung ist nur die Quadratwurzel aus der Varianz und wird nach einer festen Formel berechnet. Wir werden uns nicht die Mühe machen, die Standardabweichung zu berechnen, sondern werden damit immer die Computersoftware beauftragen.

Abb. 4-9 Normalverteilte Daten
Die Standardabweichung ist ein äußerst wichtiges Streuungsmaß, aus dem wir gemeinsam mit dem Mittelwert bereits sehr viele Informationen über die Daten gewinnen können. Unterstellen wir für die weitere Argumentation einen Mittelwert von 12 und nehmen wir jetzt an, dass die Standardabweichung in der einen Gruppe 0,1 beträgt und in der anderen Gruppe 2. Damit wissen wir, dass die Daten der zweiten Gruppe mit σ=2 deutlich mehr variieren als in der ersten Gruppe mit σ=0,1. Betrachten wir jetzt noch einmal die Abbildung 4-9. Der dunkelrote Bereich umfasst alle Daten mit µ±σ. In der ersten Gruppe wäre das der Bereich 12±0,1, also von 11,9–12,1. In der zweiten Gruppe wäre der Bereich dagegen 12±2. Er würde von 10-14 reichen.
Die Standardabweichung erlaubt uns so die Verteilung der Daten und die Breite der Glockenkurve abzuschätzen. Wichtig ist dabei auch eine prozentuale Abschätzung. Innerhalb des Bereiches µ±σ liegen nämlich 68,3 Prozent aller Daten. Innerhalb von µ±2σ liegen 95,4 Prozent aller Daten und innerhalb von µ±3σ sogar 99,7 Prozent. Wenn wir also zwei Standardabweichungen – oder genauer 1,96*σ – auf beiden Seiten des Mittelwertes abziehen bzw. addieren, dann haben wir den Bereich abgesteckt, in dem sich 95 Prozent der Daten befinden. Das ist eine wichtige Erkenntnis, die wir nicht vergessen dürfen und mit der wir später praktisch arbeiten werden.

Normal verteilte Daten lassen sich optimal mit dem Mittelwert und der Standardabweichung beschreiben. Jeder, der über ein ausreichendes Verständnis der Normalverteilung verfügt, hat sofort ein adäquates Bild vor Augen, wie die Daten verteilt sind. Bei einem Mittelwert von 60 und einer Standardabweichung von fünf befinden sich zirka 95 Prozent innerhalb des Bereiches von 50 bis 70. Bei einem Mittelwert von 200 und einer Standardabweichung von 50 befinden sich zirka 95 Prozent der Daten im Bereich von 100 bis 300. Ob die Kurve weit oder eng ist, können wir mit beiden Informationen sicher abschätzen.

Abb. 4-10 Rechtsschiefe Verteilung
Nehmen wir einmal an, dass bei einem Mittelwert von 12 die Standardabweichung sieben beträgt. Dann befinden sich 68,3 Prozent zwischen fünf und 19. Wenn wir jetzt zwei Standardabweichungen berücksichtigen wollen, stoßen wir auf ein Problem. Der Bereich (µ±2σ) beträgt jetzt -2 bis 26. Was ist aber, wenn es keine Werte geben kann, die kleiner als 0 sind? Offensichtlich handelt es sich nicht um eine normale Verteilung, die einer symmetrischen Glockenkurve ähnelt. Mit dieser einfachen Übersicht von µ±2σ können wir somit leicht entdecken, wann die Daten nicht normal verteilt sind.
Wir haben den Begriff „Normalverteilung“ bisher verwendet, um eine spezielle Verteilung von Daten zu beschreiben, an die bestimmte Bedingungen geknüpft sind, auf die wir hier nicht weiter eingehen werden. Mit den gängigen Statistikprogrammen kann für jede numerische Menge beurteilt werden, ob die Daten normal verteilt sind (z.B. Shapiro-Wilk-Test). Nicht alle Daten erfüllen diese Bedingungen, so dass manche Daten asymmetrisch oder schief verteilt sind. Sie können auch einen oder mehrere Gipfel aufweisen oder sogar gewölbt sein. Diese Verteilung können wir graphisch sichtbar machen und durch so genannte Formmaße beschreiben, von denen wir die Schiefe (skewness) und die Wölbung (courtois) kennen sollten.
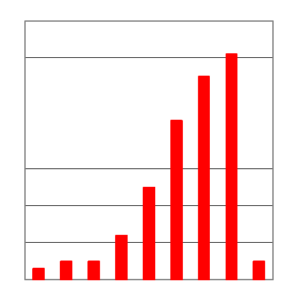
Abb. 4-11 Linksschiefe Verteilung
Wenn die Daten gleichmäßig um den Mittelwert verteilt sind, wie wir es von der Glockenkurve kennen, beträgt die Schiefe 0. Bei einer rechtsschiefen Verteilung beträgt die Schiefe über 0 und bei linksschiefen Verteilungen unter 0. Viele medizinische Merkmale sind rechtsschief verteilt (Abb. 4-10), d.h. sie haben auf der linken Seite einen hohen Gipfel und die Werte laufen nach rechts aus. Denken wir dabei an Laborwerte wie Bilirubin, alkalische Phosphatase, Kreatinin, Harnstoff. Sie können keine negativen Werte annehmen und je höher der Wert umso seltener tritt der Wert auf. Einige linksschiefe Verteilungen (Abb. 4-11) mit einem hohen rechten Gipfel und Ausläufern nach links sind zum Beispiel die Schwangerschaftsdauer oder ein Gerinnungswert (Quickwert). Bei schiefen Verteilungen differieren der Mittelwert und Medianwert zum Teil erheblich, so dass der Medianwert verlässlicher ist.
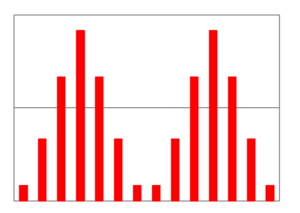
Abb. 4-12 Gewölbte Verteilung
Bei einer linksschiefen Verteilung können wir tatsächlich den obigen Witz realisieren, dass die Mehrheit der Menschen mehr verdient als der Durchschnitt. Dazu müsste der Mittelwert sich nur links vom Median befinden. In der gegenwärtigen Verteilung sorgen wenige sehr Reiche dafür, dass die Verteilung rechtsschief ist. Der Mittelwert verlagert sich nach rechts und ist dadurch größer als der Median. Wenn wir also die sehr Reichen abschaffen und stattdessen mehr richtig Arme kreieren, dann könnten wir auch hier eine linksschiefe Verteilung erreichen.
Ein weiteres Formmaß ist die Wölbung, die die Anhäufungen am Mittelwert bzw. den Enden beschreibt. Bei einer Wölbung unter 0 werden quasi die Schultern betont und der mittlere Bereich eingedrückt. Ein gutes Beispiel sind zweigipflige Daten wie bei der Geburtstagsfeier des Großvaters und der Tochter (Abb. 4-12), die wir nicht zweifelsfrei erkennen, wenn wir nur den Mittelwert und die Standardabweichung kennen.